Maksymalna elongacja planety

W dniu 21 grudnia 2022 roku o godzinie 16, Merkury będzie, z punktu widzenia ziemskiego obserwatora, najdalej oddalony od Słońca w kierunku wschodnim, czyli osiągnie maksymalną elongację wschodnią. Kąt maksymalnej elongacji wyniesie 20°08’. Odległość kątowa Merkurego od Słońca podczas grudniowej elongacji nie jest imponujący.

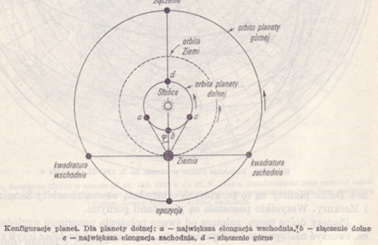
Z mechaniki nieba wiadomo, że orbita Merkurego jak i Ziemi są w przybliżeniu eliptyczne, przy czym mimośród orbity merkuriańskiej jest większy. Kiedy orbity obu planet byłyby kołowe, wówczas maksymalny kąt elongacji Merkurego wyniósł by 22°46’. W wypadku rzeczywistym tak nie jest i maksymalny kąt elongacji zmienia się. W zależności od położenia obu planet na swoich orbitach, maksymalny kąt elongacji waha się od 17°30’ do 27°50’ (w obecnych czasach). Z przeprowadzonych przez Jeana Meeusa [1] obliczeń wynika, że kąt maksymalnej elongacji zachodniej jest osiągany pod koniec marca lub na początku kwietnia, czyli w okresie, kiedy Merkury znajduje się w pobliżu aphelium swojej orbity, natomiast Ziemia znajduje się wówczas w przybliżeniu w średniej odległości od Słońca. Z przeprowadzonych obliczeń za okres 2000 – 2100 wynika, że ekstremalny maksymalny kąt elongacji zachodniej zostanie osiągnięty w następujących terminach:

30 III 2046 roku, 27°49’30” W

02 IV 2059 roku, 27°49’49,8” W

30 III 2092 roku, 27°49’43,68” W

Największy kąt elongacji wschodniej jest osiągany przez Merkurego w sierpniu, wtedy Merkury ponownie znajduje się w pobliżu aphelium swojej orbity, natomiast Ziemia znajduje się w odległości 151,47 mln km od Słońca. W XXI wieku wystąpią jeszcze cztery ekstremalnie maksymalne elongacje wschodnie Merkurego:

15 VIII 2049 roku, 27°26’04,92” E

18 VIII 2062 roku, 27°25’55.02” E

13 VIII 2082 roku, 27°25’33,24” E

16 VIII 2095 roku, 27°26’02,4” E

Jeśli spojrzy się na wartości ekstremalnych maksymalnych kątów elongacji Merkurego to zauważyć można, że kąt ten jest większy w wypadku elongacji zachodniej. Dlaczego? Odpowiedź jak zawsze znajdziemy w mechanice nieba. Otóż zarówno w terminach elongacji wschodniej jak i zachodniej Merkury znajduje się praktycznie w aphelium swojej orbity i odległość Merkurego od Słońca jest w przybliżeniu taka sama. Natomiast odległość Ziemi od Słońca, w obu rozpatrywanych terminach, jest różna. W terminach końca marca Ziemia znajduje się w odległości około 149,5 mln km, natomiast w terminie sierpniowym Ziemia jest w nieco większej odległości, 151,47 mln km. Ta różnica w odległości Ziemi od Słońca powoduje, że różnica maksymalnych kątów elongacji wschodniej i zachodniej osiąga wartość rzędu 0°24’.

Orbity obu planet są perturbowane i wzajemne położenie peryheliów Merkurego i Ziemi się zmienia. Długość peryhelium orbity Ziemi zmienia się z prędkością 0,3226° na stulecie, natomiast długość peryhelium orbity Merkurego zmienia się z prędkością 0,1589° na stulecie. Skutkuje to tym, że względne położenie obu peryheliów zwiększa się. Z obliczeń obejmujących dłuższy okres czasu wynika, że różnica pomiędzy dwoma ekstremalnymi kątami elongacji (wschodniej i zachodniej) wynosiła w przeszłości jedynie około 21’:

Elongacja wschodnia: 11 VII – 906 rok, 27°25’24,6” E

Elongacja zachodnia: 23 II – 906 rok, 27°46’19,92” W

W LI wieku, jeśli do tego czasu ludzkość przetrwa, różnica obu kątów osiągnie wartość około 26’:

Elongacja wschodnia: 30 IX 5093 roku, 27°27’ 9,72” E

Elongacja zachodnia: 17 V 5057 roku, 27°52’49,08” W

Kąty obu maksymalnych elongacji – wschodniej i zachodniej – byłyby równe tylko wówczas, kiedy orbita Ziemi byłaby okręgiem. Z mechaniki nieba wiadomo, że w chwili obecnej mimośród orbity ziemskiej zmniejsza się i orbita staje się coraz bardziej zbliżona do okręgu. Najbliższe minimum mimośrodu orbity ziemskiej, o wartości e=0,0023, zostanie osiągnięte w 29500 roku.

Z obliczeń przeprowadzonych na okres 2010 – 2040 [2] wynika, że najmniejsze wartości elongacji były osiągnięte 7 stycznia 2022 roku, kiedy to podczas elongacji wschodniej Merkury oddalił się maksymalnie od Słońca na wschód na odległość 19°13’ E oraz 8 października 2022 roku podczas elongacji zachodniej, kiedy to Merkury oddalił się od Słońca na zachód na odległość 17°59’ W. W przyszłym roku 11 kwietnia 2023 roku Merkury oddali się od Słońca na wschód na odległość 19°29’E podczas elongacji wschodniej oraz 22 września 2023 roku, kiedy to podczas elongacji zachodniej Merkury oddali się od Słońca na zachód na odległość 17°52’W.  Najmniejsze wartości kąta elongacji są osiągane wówczas, kiedy Merkury znajduje się w pobliżu peryhelium swojej orbity.

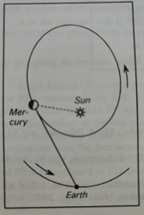
Merkury oraz Wenus podobnie jak i Księżyc przechodzi przez cykl faz. Kiedy planety znajdują się między Słońcem, a Ziemią, czyli wtedy, kiedy jest koniunkcja dolna, wówczas planeta (Merkury, Wenus) są w fazie nowiu. Kiedy planety znajdują się po przeciwnej stronie Słońca są w koniunkcji górnej, wówczas znajdują się w fazie pełni. Podczas ruchu orbitalnego występują takie dwa położenia planety, które dla obserwatora ziemskiego są w maksymalnej elongacji wschodniej lub zachodniej. Czyli teoretycznie powinny być w fazie kwadry, co powinno objawić się tym, że obserwator widziałby tarczę planety oświetloną w 50%.

Mechanika powstawania faz planet wewnętrznych na przykładzie Wenus. Źródło: Stanisław R. Brzostkiewicz, Wenus siostra Ziemi, Nasza Księgarnia, 1988

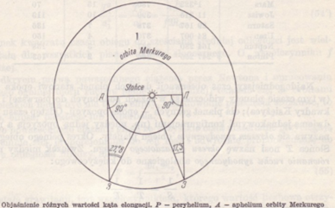
Czy tak jest rzeczywiście? Otóż, kiedy orbity obu planet byłyby kołowe wówczas byłoby to prawdą. Rzeczywistość jest inna. Rozważymy to na przykładzie Merkurego, gdyż ta planeta jest bohaterem naszego niebiańskiego spektaklu. Jak już wspomniano wcześniej orbity Merkurego i Ziemi są w przybliżeniu eliptyczne. Mimośród orbity Merkurego jest największy spośród ośmiu planet w naszym układzie Słonecznym i wynosi e=0,20564. Mimośród orbity Ziemskiej jest mniejszy i wynosi e=0,01671. W zależności od położenia planet na orbitach względem ich peryheliów, podczas maksymalnej elongacji wschodniej lub zachodniej, powierzchnia planety wewnętrznej może być oświetlona powyżej lub poniżej 50 %. Maksymalna elongacja planety nie zbiega się z fazą kwadry, chociaż w wyniku sprzyjających okoliczności może tak się zdarzyć. Z przeprowadzonych obliczeń [3] wynika, że wielkość oświetlonej powierzchni planety Merkurego podczas maksymalnej elongacji wynosi:

a) największa elongacja wschodnia: F= 0,368 – 0,634;

b) największa elongacja zachodnia: F=0,365 – 0,638;

c) przy czym dla ekstremalnego kąta elongacji wielkość oświetlenia zmienia się w granicach: F=0,3676 – 0,6340.

Dla Wenus wielkość oświetlenia powierzchni planety, podczas maksymalnej elongacji wschodniej lub zachodniej, nieznacznie różni się od 50 %, a to za sprawą małego mimośrodu jej orbity, który wynosi e=0,00678. Wielkość oświetlenia podczas maksymalnej elongacji waha się od F=0,487 (podczas elongacji w dniu 24 VIII 1994 roku), do F=0,512 (podczas elongacji w dniu 17 I 2001 roku).

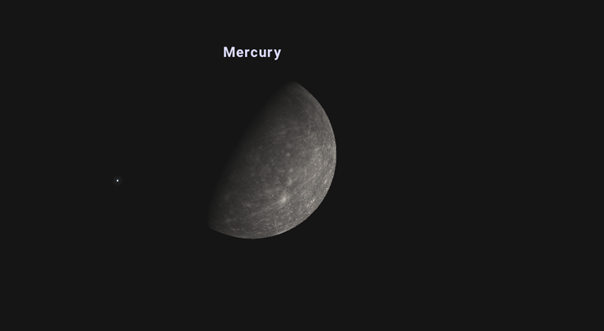
Warunki widzialności w dniu 21 XII 2022 roku

Na załączonej mapie nieba przedstawiono położenie Merkurego, w chwili osiągnięcia przez planetę maksymalnej elongacji wschodniej. Merkury będzie znajdował się w konstelacji Strzelca. Niestety, ale niebo nie będzie ciemne. Co prawda Słońce znajdzie się już pod horyzontem, ale do godziny 16:07 będzie jeszcze pod horyzontem na głębokości mniejszej niż 6° (dla Warszawy), czyli będzie wówczas panował zmierzch cywilny (dla innych rejonów naszego kraju zmierzch żeglarski rozpocznie się w nieco innym czasie). Merkury zajdzie około godziny 16:54 (w rejonie Polski centralnej, Łódź).

Kiedy spojrzymy przez lunetę wówczas spostrzeżemy, że w 61% tarcza Merkurego będzie oświetlona (czyli będzie w fazie Merkurego garbatego malejącego).

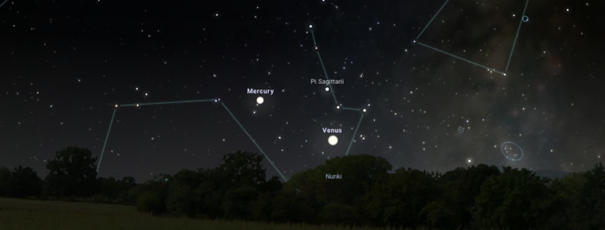
W poszukiwaniu pierwszej gwiazdki

Podczas tegorocznej Wigilii, w oczekiwaniu na Św. Mikołaja, możemy spojrzeć na wieczorne niebo, które w tym roku będzie obfitowało w wiele atrakcji. Około 47 minuty po zachodzie Słońca, uważny obserwator (w razie bezchmurnej pogody) będzie mógł na zachodzie dostrzec Księżyc, Wenus i Merkurego tworzące trójkąt równoramienny. Rosnący Księżyc będzie oddalony o 7 stopni od Wenus (i uformują podstawę tego trójkąta), natomiast Merkury będzie stanowił górny wierzchołek, oddalony o około 4 stopnie od pozostałych wierzchołków.

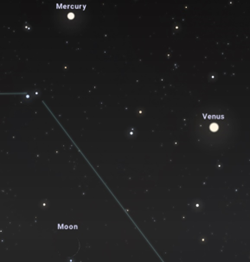
Merkury osiągnie jasność około -0.31 mag, w 50% będzie oświetlona jego powierzchnia, czyli będzie w fazie kwadry. Wenus zajaśnieje nam tego wieczora z mocą -3.91 mag, a jej powierzchnia będzie oświetlona w 96,662%, czyli będzie w fazie Wenus garbatej malejącej. Księżyc natomiast będzie półtora dnia po nowiu (w fazie rosnącego sierpa) i będzie oświetlony zaledwie w 2,302%. Jasność Księżyca osiągnie wartość około -5,9 mag.

Rozmaitości o Merkurym

Tranzyty Merkurego

Z Merkurym jako planetą wewnętrzną (podobnie jak Wenus), związane jest także inne zjawisko – przejścia przed tarczą Słońca. Dzieje się tak, gdy mamy złączenie dolne i Merkury znajduje się w pobliżu węzła swojej orbity, tj. przecina płaszczyznę orbity Ziemi wokół Słońca. Ostatni raz takie zjawisko miało miejsce 11 listopada 2019 r. Następne wystąpią 13 listopada 2032 roku i 7 listopada 2039 r. Tarcza Merkurego widziana w takim tranzycie to zaledwie 1/200 średnicy tarczy słonecznej. Samo zjawisko trwa kilka godzin.

Tranzyty Merkurego na tle tarczy słonecznej równiej mogły by być obserwowane z powierzchni Wenus oraz z innych planet zewnętrznych. Na przykład dla obserwatorów z Wenus ostatnie takie zjawisko miało miejsce 2 lipca 2022 roku, wówczas Merkury znajdował się w pobliżu węzła wstępującego swojej orbity (względem orbity wenusjańskiej). Następne będzie miało miejsce 16 stycznia 2028 roku, w pobliżu tego samego węzła orbity [4]. Czas trwania tranzytu jest podobny do ziemskiego. Podczas tranzytu przez centrum planety zjawisko będzie trwało 6,2 godzin. Merkury – jako najbliższa Słońcu planeta – ma także najwyższą prędkość orbitalną, rzędu 39 – 59 km/s. Dla porównania, Ziemia osiąga „zaledwie” 30 km/s. Jednak ruch całego Układu Słonecznego przez Galaktykę ma prędkość rzędu kilkuset km/s. Jednego pełnego obiegu wokół Słońca Merkury dokonuje w ciągu prawie 88 dni ziemskich.

Niebo widziane z Merkurego

Merkury wiruje wokół własnej osi bardzo powoli. Okres rotacji wynosi 58,6461 dnia co pozostaje w rezonansie 3:2 z ruchem obiegowym, czyli na dwa obiegi Merkurego przypadają trzy obroty wokół własnej osi. Merkuriańska doba słoneczna jest długa i trwa 175,938 dnia. Czyli doba słoneczna trwa dwa lata merkuriańskie. Obserwatorzy merkuriańskiego nieba mogą spostrzec dość dziwny ruch Słońca na niebie, kiedy planeta znajduje się w pobliżu peryhelium orbity. Otóż, kiedy planeta znajduje się w pobliżu peryhelium porusza się z prędkością liniową większą od prędkości liniowej punktu znajdującego się na powierzchni obracającej się wokół swojej osi planety.  Słońce, kiedy planeta zbliża się do peryhelium, zaczyna pozornie na niebie hamować osiągając punkt, w którym jest statyczne (prędkość liniowa na orbicie została zrównana z prędkością liniową punktu na powierzchni planety), następnie Słońce zaczyna się pozornie cofać (tzw. ruch retrogradacyjny, czyli wsteczny). Prędkość kątowa Słońca w ruchu retrogradacyjnym na niebie jest maksymalna w chwili, kiedy Merkury znajduje się dokładnie w peryhelium orbity. Następnie Słońce zaczyna hamować i osiąga ponownie punkt stacjonarny (przy ponownym zrównaniu prędkości liniowych planety na orbicie i punktu na powierzchni planety). Z chwilą, kiedy prędkość orbitalna zaczyna być mniejsza niż prędkość punktów na powierzchni planety, Słońce zaczyna poruszać się ruchem dyrekcyjnym, czyli prostym. W ciągu tych kilku dni ziemskich (8 dni z czego 4 dni przypada na okres przed przejściem Merkurego przez peryhelium i następne 4 dni to okres po przejściu planety przez peryhelium) Słońce na merkuriańskim niebie zatacza pętle wielkości 1° [5]. Na obszarach, gdzie następuje np. wschód Słońca, położenie planety w peryhelium może spowodować fascynujące zjawisko. Kiedy Słońce rozpoczyna wyłanianie się spod horyzontu wschodzi tylko częściowo. Następnie po rozpoczęciu ruchu retrogradacyjnego zachodzi. Po kilku dniach ziemskich, kiedy Słońce rozpocznie ruch prosty, zaczyna ponownie wschodzić. Podobnego wrażenia obserwator doświadczy w obszarach planety, gdzie zachodzi Słońce, w odwrotnej kolejności. Oś obrotu planety odchylona jest od prostopadłej do płaszczyzny orbity jedynie o 0,034°. Takie położenie osi obrotu planety wokół własnej osi sprawia, że obserwator rezydujący na biegunie widziałby Słońce znajdujące się w pobliżu horyzontu. Słońce mogłoby wznieść się nad horyzont jedynie na wysokość 2’2”. I na taką samą głębokość schować się pod horyzontem. Mieszkaniec równika, widział by Słońce, które podczas kulminacji górnej praktycznie zawsze znajduje się w pobliżu zenitu.

Ruch precesyjny peryhelium Merkurego (Ta część opracowania przeznaczona dla zaawansowanych miłośników astronomii)

W zagadnieniu dwóch ciał, orbity po których się poruszają się ciała są ściśle określone i są to krzywe stożkowe. Takie rozwiązania nazywa się dokładnymi. W rzeczywistym Układzie Słonecznym nie mamy układu dwóch ciał. Mamy Słońce i wiele innych ciał, rozmiarowo mniejszych od Słońca. Ciała te oddziałują ze Słońce zgodnie z prawem Newtona oraz oddziałują między sobą, perturbując swoje orbity. To powoduje, że żadne ciało nie porusza się po dokładnej krzywe stożkowej. W celu opisania ruchu i wyznaczenia toru ciała obiegającego Słońce w obecności innych ciał do siły oddziaływania grawitacyjnego, należy dodać wiele poprawek, które co prawdą nie są duże, ale wystarczające, aby spowodować, że orbita, po której porusza się planeta czy inny obiekt wokół ciała centralnego, różni się od rozwiązania dokładnego, czyli od krzywej stożkowej.

Rozważmy przypadek, kiedy ciało porusza się po orbicie eliptycznej. W wypadku orbity eliptycznej ciało może poruszać w pewnym ograniczonym obszarze, tor po którym porusza się planeta całkowicie znajduje się wewnątrz pierścienia ograniczonego okręgami, których promienie równe są odległości planety w peryhelium i aphelium. Można zadać pytanie czy taki tor będzie krzywą zamkniętą. Tor będzie zamknięty tylko i wyłącznie w sytuacji, kiedy ciało będzie poruszało się w polu, którego potencjał pola jest odwrotnie proporcjonalny do odległości lub proporcjonalny do kwadratu odległości. Pierwszy wypadek i on jest dla nas istotny z punktu widzenia rozpatrywanego zagadnienia, odpowiada dokładnie ruchowi ciała w polu centralnym (w polu grawitacyjnym lub elektrostatycznym), czyli zagadnieniu Keplera. Rozważymy tylko ruch w polu grawitacyjnym.  W układzie Słonecznym, jak już wspomniano wcześniej, na ciało nie działa jedynie siła oddziaływania grawitacyjnego pochodząca od Słońca, ponieważ nie jest to zagadnienie dwóch ciał tylko tak naprawę jest to zagadnienie wielu ciał. W tym wypadku tor ruchu takiego ciała nie jest krzywą zamkniętą. Oznacza to, że jeżeli ciało rozpocznie ruch np. z peryhelium wówczas po jednym pełnym obiegu nie powróci do punktu wyjściowego. Równanie otrzymanego toru jest jednocześnie równaniem krzywej płaskiej, którą w geometrii różniczkowej identyfikujemy jako rozetę. Z mechaniki nieba wiadomo, że taki rozetkowy tor jest stabilny co oznacza, że poruszające się ciało nie opuści obszaru pierścienia, którego rozmiary określone są odległościami planety w peryhelium i aphelium. Orbita taka nigdy jednak nie będzie krzywą zamknięta. W ciągu jednego pełnego obiegu linia apsyd (czyli linia łącząca skrajne punkty na orbicie – peryhelium i aphelium) zakreśli pewien kąt. To wiekowe przesunięcie peryhelium orbity nazywa się precesją peryhelium.

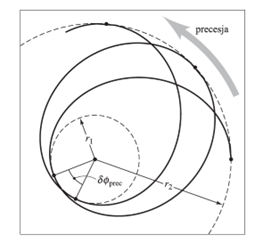
W wypadku Merkurego prędkość kątowa peryhelium, wyznaczona w oparciu o newtonowską teorię grawitacji, spowodowana oddziaływaniem planet wywołujących perturbację orbity Merkurego okazała się mniejsza o 43” na stulecie od wartości zmierzonej. Całkowite przesunięcie peryhelium orbity Merkurego wynosi 5599,74” ± 0,41” na stulecie. Z czego 5025,645” ± 0,50” na stulecie przypada na precesję astronomiczną, związaną z precesją osi ziemskiej, skutkiem której jest precesja punktu równonocy wiosennej, który jest punktem względem, którego wyznaczane jest położenie peryhelium orbity. Przesunięcie peryhelium o wartości 531,54”±0,68” na stulecie jest konsekwencją perturbacji planetarnych. Największy wkład pochodzi od Wenus, która perturbując orbitę Merkurego wywołuję precesję jego peryhelium o wartości 277,856” na stulecie. Drugim obiektem znacząco perturbującym orbitę planety i dającym wkład do przesunięcia peryhelium o wartości 153,584” na stulecie jest Jowisz. Trzecim istotnym obiektem zaburzającym orbitę Merkurego jest Ziemia, która daje wkład o wartości 90,038” na stulecie do precesji jego peryhelium. Po zsumowanie efektów pochodzącym od głównych planet zaburzających ruch planety otrzymuje się łączną wartość 5557,18”±0,85” na stulecie. Odejmując od siebie wartości zmierzoną i sumaryczną, pochodzącą od istotnych obiektów zaburzających ruch planety, otrzymuje się wartość 42,45”±0,94” na stulecie, której źródło nie potrafi wyjaśnić newtonowska mechanika nieba. Kiedy przeprowadzi się rozważania na gruncie szczególnej teorii względności, gdzie punktem wyjścia będzie relatywistyczna całka energii to otrzymane przesunięcie peryhelium Merkurego i tak będzie za małe, bo zaledwie 7” na stulecie [6]. Szczególna teoria względności podobnie jak newtonowska mechanika nieba nie jest wstanie wytłumaczyć efektu. Rozwiązanie zagadki przyniosła dopiero ogólna teoria względności, czyli relatywistyczna teoria grawitacji. Słońce, jak każde ciało masywne modyfikuje czasoprzestrzeń, zakrzywiając ją. Należy podkreślić, że każde ciało powoduje zakrzywienie czasoprzestrzeni, nawet Ziemia, ale ze względu na niewielką masę i rozmiary ciała, to zakrzywienie nie jest istotnie duże.  Łatwo to sobie można wyobrazić wykonując proste domowe doświadczenie. Wystarczy rozciągnąć powłokę gumową. Kiedy na powłoce gumowej nie zostanie umieszczone żadne ciało, powłoka będzie płaska. Co odpowiada sytuacji próżni. Kiedy na powłoce gumowej umieścimy metalową kulkę wówczas powłoka odkształci się. Im będzie większa i masywniejsza tym odkształcenie będzie większe. Sytuacja analogiczna do rozważanej powyżej, dotyczącej odkształcenia czasoprzestrzeni przez Słońce i Ziemię. Kiedy przeanalizuje się trajektorię ruchu Merkurego z punktu widzenia teorii grawitacji Einsteina, to okazuję się, że otrzymana wartość przesunięcia peryhelium na gruncie ogólnej teorii względności doskonale zgadza się z wartością, której źródła do tej pory nie mogły wyjaśnić ani newtonowska mechanika nieba, ani szczególna teoria względności [7, 8, 17].

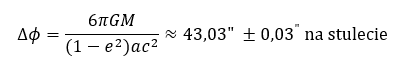
gdzie: M – masa ciała centralnego, w naszym wypadku Słońca, G – stał grawitacji, c – prędkość światła, e – mimośród orbity planetarnej, a – wielka półoś orbity planety.

Zakrzywienie czasoprzestrzeni skutkuje pojawieniem się dodatkowego przyspieszenia, oprócz newtonowskiego przyspieszenie grawitacyjnego. Poprawkę relatywistyczną otrzymuje się w wyniku sferycznie symetrycznego rozwiązania Schwarzschilda równań grawitacji Einsteina. Otrzymana poprawka silnie zależy od odległości, a mianowicie maleje z czwartą potęgą odległości, co skutkuje tym, że wpływa jedynie w sposób istotny na ruch Merkurego. Dla pozostałych planet efekt jest mniejszy. Na przykład dla Wenus dodatkowe przesunięcie peryhelium wynikające z teorii grawitacji Einsteina wynosi 8,63” na stulecie.  Obserwacje dają wartość 8,4”±4,8” na stulecie. Po raz kolejny widać dobrą zgodność teorii z doświadczeniem. Dla Ziemi dodatkowe przesunięcie peryhelium wynikające z ogólnej teorii względności wynosi zaledwie 3,84” na stulecie. Pomiary astronomiczne dają wartość rzędu 4,6”±2,7” na stulecie. W wypadku Ziemi całkowity kąt precesji peryhelium wynosi 6183,7” ±1,1” na stulecie. Precesja astronomiczna oraz precesja wynikająca z perturbacji planetarnych wynosi dla Ziemi 6179,1”±2,5” na stulecie. Dla Marsa teoria grawitacji Einsteina przewiduje dodatkową precesję jego peryhelium rzędu 1,35” na stulecie. Dla Jowisza wartość ta jest jeszcze mniejsza, co jest w zgodzie ogólną teorią względności i wynosi 0,06” na stulecie [8]. Dla pozostałym planet efekt ten jest jeszcze mniejszy i pozostaje po za granicami dokładności pomiarowych.

Zakrzywienie czasoprzestrzeni przez masywne ciało również wpływa na tor światła powodując jego odchylenie od toru pierwotnego. Odchylenie promieni świetnych, których źródłem są odległe gwiazdy, przez masywne centra pola grawitacyjne, objawia się pozornym przesunięciem ich położenia.

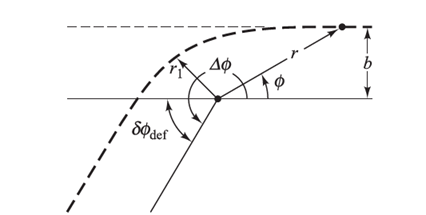
Pierwsze próby wyjaśnienia tego zjawiska na gruncie nierelatywistycznej mechaniki nie przyniosły zadawalających rezultatów. Otrzymany kąt odchylenia promieniowania elektromagnetycznego był dwukrotnie za mały w porównaniu z wartościami rzeczywistymi.

 Poprawne wyjaśnienie tego efektu otrzymano na gruncie relatywistycznej teorii grawitacji, czyli ogólnej teorii względności. Dopiero relatywistyczna teoria grawitacji w sposób poprawny opisuje oddziaływanie pola grawitacyjnego i fal elektromagnetycznych.  Otrzymana wartość kąta zakrzywienia promienia świetlnego w wyniku jego przejścia w pobliżu centrum grawitacji wynosi [7]:

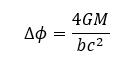
gdzie: M – masa ciała centralnego, w naszym wypadku Słońca, G – stał grawitacji, c – prędkość światła, b – odległość promienia świetlnego od centrum grawitacji, w wypadku Słońce jest to promień gwiazdy.

Dla promieni światła przechodzących w pobliżu krawędzi tarczy Słonecznej teoretyczna wartość kąta wynosi 1,75”.  W celu jej potwierdzenia zorganizowano ekspedycję pod przewodnictwem sir prof. Artura Eddingtona. Celem ekspedycji było potwierdzenie ogólnej teorii względności Einsteina, poprzez weryfikację obliczonych teoretycznie kątów ugięcia, spowodowanych przez Słońce, promieni świetlnych pochodzących od gwiazd. W dniu 29 maja 1919 roku miało nastąpić zaćmienie Słońca. Miało to być zaćmienie całkowite należące do serii zaćmień ze 136 cyklu Saros. Geocentryczne złączenie Słońca i Księżyca w rektascensji miało nastąpić o 13^h 08^m 55^s czasu UTC, a maksymalna faza zaćmienia miała trwać 6^m51^s. Podczas zaćmienia skupiono się na obserwacji grupy gwiazd o nazwie Hiady. Hiady to gromada otwarta gwiazd, znajdująca się w konstelacji Byka, niedaleko Aldebarana, będącego najjaśniejszą gwiazdą w tym gwiazdozbiorze. Eksperyment przebiegał dwuetapowo. W nocy dokonano dokładnych pomiarów położeń gwiazd. W drugim etapie, podczas zaćmienia Słońca, pomiary powtórzono. Podczas zaćmienia Hiady znajdowały się dokładnie za Słońcem. Pomiary, a dokładniej fotografowanie Słońca i Hiad, rozpoczęto o godzinie 14¹⁵. Podczas eksperymentu wykorzystano aż szesnaście płyt fotograficznych. Liczba zdjęć została uzupełniona dziewiętnastoma zdjęciami wykonanymi przez Crommelina i Davidsona. W oparciu o zdjęcia Eddingtona wyznaczono kąt ugięcia światła, którego wartość była równa 1,61”±0,3”, co z grubsza potwierdzało wynik teoretyczny 1,75”. Wyniki otrzymane w oparciu o dodatkowe zdjęcia okazały się niezgodne z ogólną teorią względności, gdyż kąt ugięcia promieni świetlnych został oszacowany na poziomie 0,93”, a to znacznie odbiegało od wartości teoretycznych. Błąd tkwił nie w teorii, a wadliwej optyce [9]. Dodatkowe dane, które zostały zebrane przez teleskop z Sobral wykazały, że kąta ugięcia wynosi 1,98”±0,16”, co było zgodne z teorią grawitacji Einsteina.

Zgodność wartości pomiarowych kąta ugięcia promieni światła przez Słońce oraz precesji peryhelium Merkurego, wywołanych efektami relatywistycznymi, z obliczeniami teoretycznymi, było dowodem na prawdziwość najpiękniejszej teorii w fizyce teoretycznej jaką jest ogólna teoria względności Einsteina.

Fizyka Merkurego

Merkury porusza się po orbicie zbliżonej do eliptycznej, nachylonej do ekliptyki pod kątem 7,005°. Mimośród orbity planety jest największy spośród wszystkich mimośrodów orbit planet w naszym układzie Słonecznym i wynosi e=0,24084. Średnia odległość planety od Słońca wynosi 57,91 mln km. Jednego pełnego obiegu wokół Słońca dokonuje w czasie 87,97 dni. Okres obrotu Merkurego wokół własnej osi wynosi 58 dni 15 godzin 26 minut. Jak już wspomniano wcześniej okres obiegu wokół Słońca i okres wirowania planety wokół własnej osi pozostają w rezonansie 3:2. Czyli trzem obrotom wokół własnej osi odpowiadają dwa obiegi planety wokół Słońca. A więc przy każdym drugim położeniu Merkurego w peryhelium planeta byłaby zwrócona tą samą stroną ku Słońcu. Doba Słoneczna na Merkurym trwa 2 lata merkurjańskie i wynosi 176 dni. Oś obrotu planety odchylona jest od prostopadłej do płaszczyzny orbity jedynie o 0,034°. Albedo powierzchni planety wynosi 0,142. Atmosfera Merkurego jest bardzo rozrzedzona. Ciśnienie przy powierzchni gruntu planety wynosi 10^-12 hPa. Merkury posiada niestabilną egzosferę złożoną z tlenu, sodu, potasu, helu, wapnia oraz wodoru. Natomiast atmosfera zbudowana jest głównie z helu, magnezu, tlenu, wodorotlenków, potasu, wody, krzemu, wapnia oraz jonów O⁺, H2O⁺, OH^–. Na Merkurym – pomimo bliskości Słońca – istnieją rejony, w których panuje wieczny cień. Są to dna kraterów w pobliżu biegunów planety. Z kolei reszta planety, wobec praktycznego braku atmosfery, doświadcza silnych kontrastów temperatury. Różnica między temperaturą dnia i nocy potrafi osiągać kilkaset stopni Celsjusza (dokładnie, między -173°C w dnach kraterów do 427°C w merkuriańskie południe). Jego orbita jest też mocno wydłużona, co też wpływa na cykl wzrostów i spadków temperatury. W aphelium temperatura powierzchni w merkuriańskie południe jest o 100°C niższa w porównaniu do temperatury powierzchni planety znajdującej się w peryhelium [10]. 

Do Merkurego wysłano z powodzeniem kilka sond, takich jak Mariner 10, Messenger, MPO (Mercury Planetary Orbiter), MIO (Mercury Magnetospheric Orbiter) czy w przed kilku laty – BepiColombo, nazwane tak od włoskiego naukowca i inżyniera Giuseppe Colombo (który opracował strategię lotu na Merkurego, polegającą na serii coraz większych zbliżeń sondy do tej planety).

Zdjęcia wykonane przez sondy pozwoliły ustalić szereg faktów z historii i chwili obecnej najbliższej Słońcu planety. Wynika z nich, że przed około 4 mld lat Merkury – podobnie jak Księżyc czy Mars – przeżył erę ciężkiego bombardowania, gdy część materii wczesnego Układu Słonecznego nie była w stanie uformować planet. Znaleziono też ślady aktywności wulkanicznej na planecie. Merkury ma też wyjątkowo wysoką średnią gęstość, podobną do Ziemi i Wenus.

Możliwe, że wnętrze Merkurego, stygnąc o kilkaset K, skurczyło się o kilkaset km [11]. Świadczą o tym „rozmyte” kratery na powierzchni planety. Z kolei w pobliżu biegunów znaleziono także lód wodny, pomimo raczej ekstremalnych temperatur wokoło. To czyni Merkurego podobnym do Marsa i Ziemi.

Wysoka gęstość średnia Merkurego oraz pomiary spektroskopowe nasunęły wniosek, że Merkury zawiera najwięcej żelaza i niklu spośród planet Układu Słonecznego. Żelazowo-niklowe jądro stanowi 75 % promienia planety. Wewnętrzna część jądra jest stała i ma rozmiary 2000 km. Zewnętrzne jądro jest płynne i ma grubość około 1000km [12]. Niektórzy badacze twierdzą, że Merkury posiada jeszcze jedną warstwę jądra stałego otaczającego część płynną jądra, złożoną z żelaza i siarki [13,14].

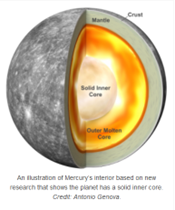
Krzemowy płaszcz planety posiada grubość około 500-700 km, natomiast skorupa planety ma rozmiary rzędu 100-300 km [12].

Literatura

1. Jean Meeus, Mathematical Astronomy Morsels IV, 2007, Willmann-Bell, Inc.
2. Jean Meeus, Astronomy Tables Of The Sun, Moon and Planets, Third Edition, 1983-2015, Willmann-Bell, Inc.
3. Jean Meeus, More Mathematical Astronomy Morsels, 2002, Willmann-Bell, Inc.
4. Jean Meeus, Transits, 1989, Willmann-Bell, Inc.
5. Zbigniew Dworak, Z astronomią za pan brat, 1989. Iskry, Warszawa.
6. Grzegorz Białkowski, Mechanika klasyczna, mechanika punktu materialnego i bryły sztywnej, 1975. PWN, Warszawa.
7. Lew. D. Landau, Jewgienij M. Lifszyc, Teoria Pola, wyd. IV, 2009, PWN.
8. Andrzej K. Wróblewski, Janusz A. Zakrzewski, Wstęp do fizyki, tom II, część I, 1989, PWN, Warszawa.
9. Pedro G. Ferreira, Teoria doskonała, stulecie geniuszy i bitwa o ogólną teorię względności, 2015, Prószyński i S-ka, Warszawa.
10. Hannau Karttunen, Pekka Kroger, Heikki OJa, Markku Poutanwen, Karl Johan Donner, Astronomia ogólna, PWN, 2020
11. Paweł Artymowicz, Astrofizyka układów planetarnych, PWN, Warszawa, 1995.
12. Antonio Genova: Scientists find evidence Mercury has a solid inner core. American Geophysical Union, 2019
13. Steven A. Hauck II. The curious case of Mercury’s internal structure. „Journal of Geophysical Research: Planets”. 118, s. 1204-1220, 2013-06-05. DOI: 10.1002/jgre.20091
14. Sean C. Solomon, Larry R. Nittler, Brian J. Anderson, Mercury: The View after Messenger, 2018, Cambridge University Press.
15. P. G. Kuligowski, Poradnik Miłośnika Astronomii, PWN, 1976
16. Stanisław R. Brzostkiewicz, Wenus siostra Ziemi, Nasza Księgarnia, 1988.
17. James B. Hartle. Grawitacja. Wprowadzenie do ogólnej teorii względności Einsteina, Wydawnictwo Uniwersytetu Warszawskiego, 2010.

Opracowanie:

dr Grzegorz Duniec, Centrum Modelowania Meteorologicznego IMGW-PIB

dr Marcin Kolonko, Centrum Modelowania Meteorologicznego IMGW-PIB

Prognoza pogody z dnia 21.12.2022

Prognoza pogody z dnia 19.12.2022

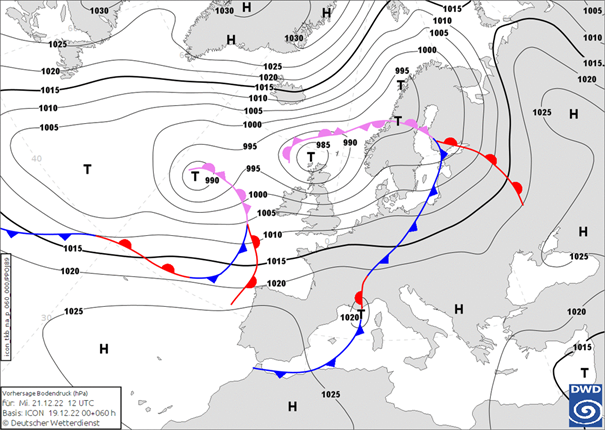
Sytuacja synoptyczna: Polska będzie pod wpływem układu niskiego ciśnienia, z centrum 985 hPa nad wyspami Lewisa. Niż będzie w stadium okludowania i wypełnienia. Z zachodu na wschód będzie przemieszczał się chłodny front atmosferyczny. Wschodnie rejony Polski jeszcze w zasięgu ciepłego wycinka układu cyklonalnego.

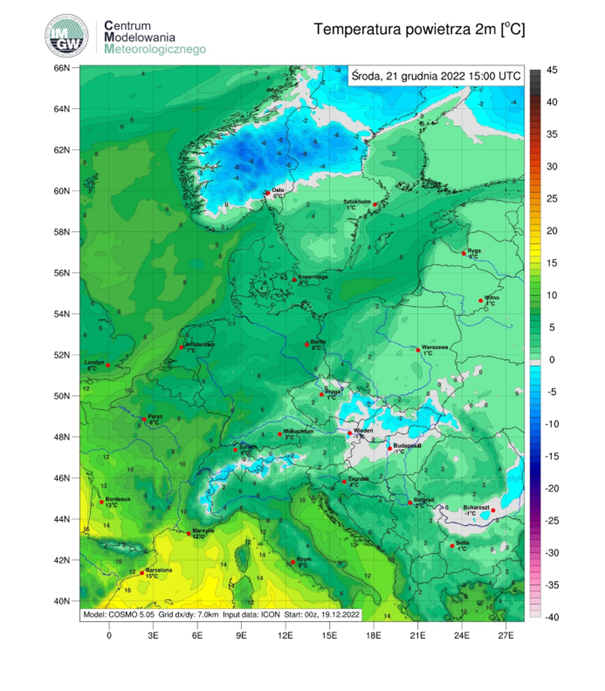
Temperatura powietrza: od 0 st. C w południowo-wschodniej Polsce do 5 – 6 st. C w północno-zachodnim rejonie kraju.

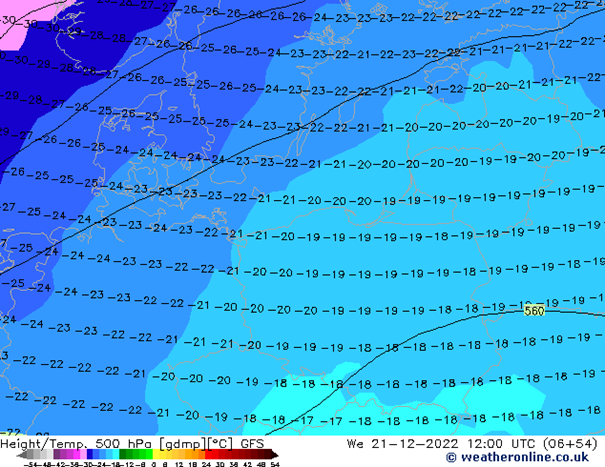
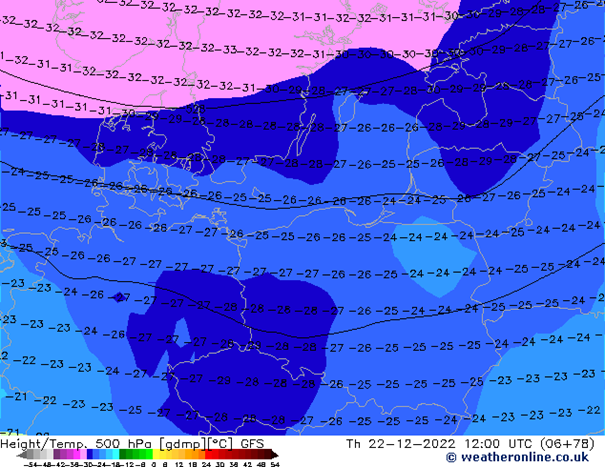
Na wysokości 5,5 km widoczny napływ zatoki chłodnego powietrza. W ciągu 24 godzin temperatura powietrza na tej wysokości spadnie o 5 – 8 st. C.

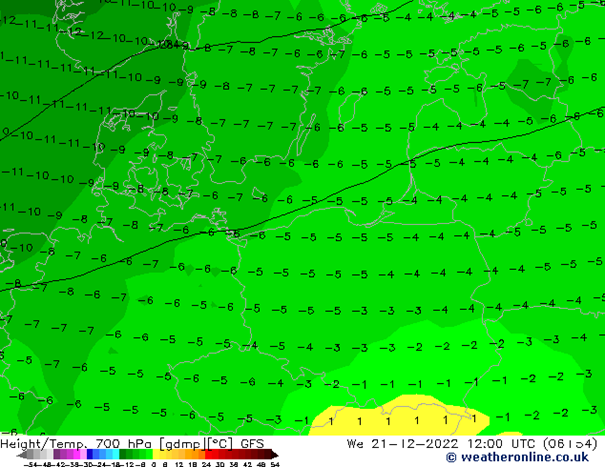
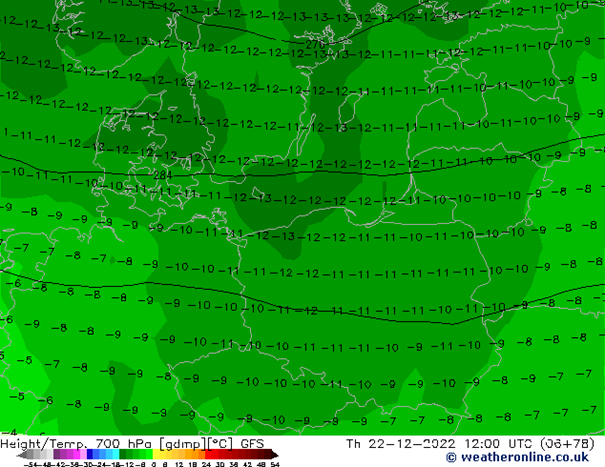
Podobny trend temperatury obserwuje się na wysokości 3 km. W ciągu doby temperatura powietrza spadnie o -8 /-10 st. C.

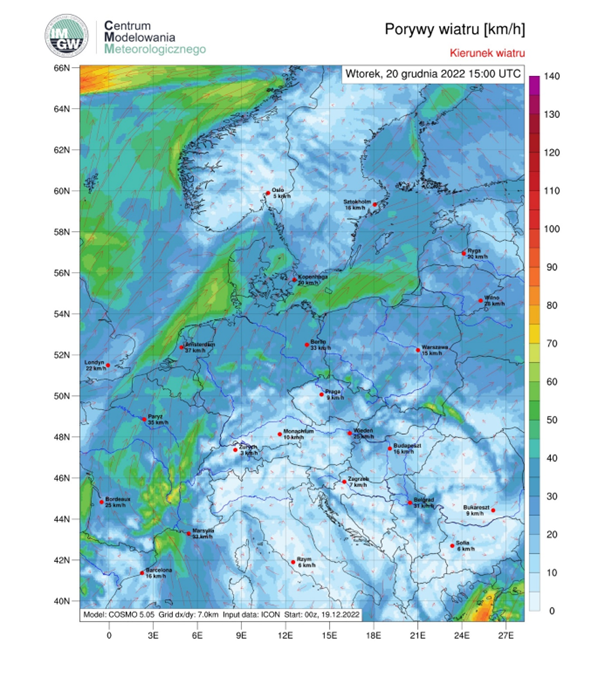
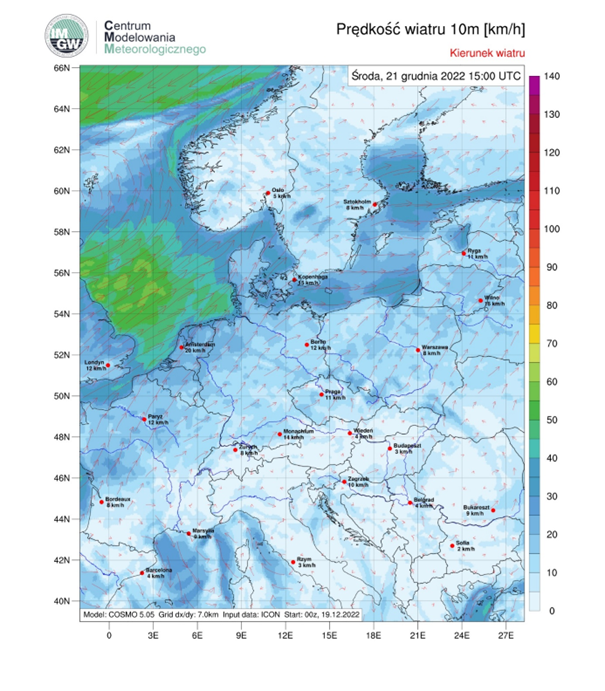
Wiatr: południowo-zachodni, 5-20 km/h. W porywach do 70 km/h na południu kraju.

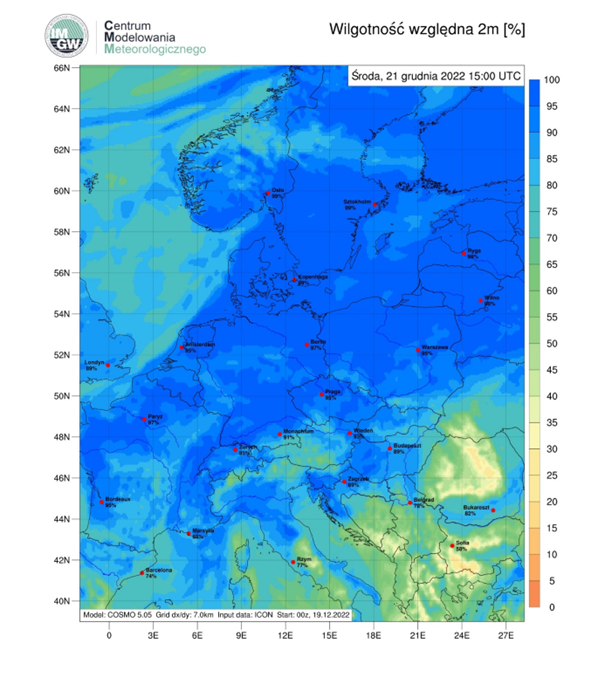
Wilgotność powietrza: 50-97%. Na przeważającym obszarze kraju powyżej 90%.

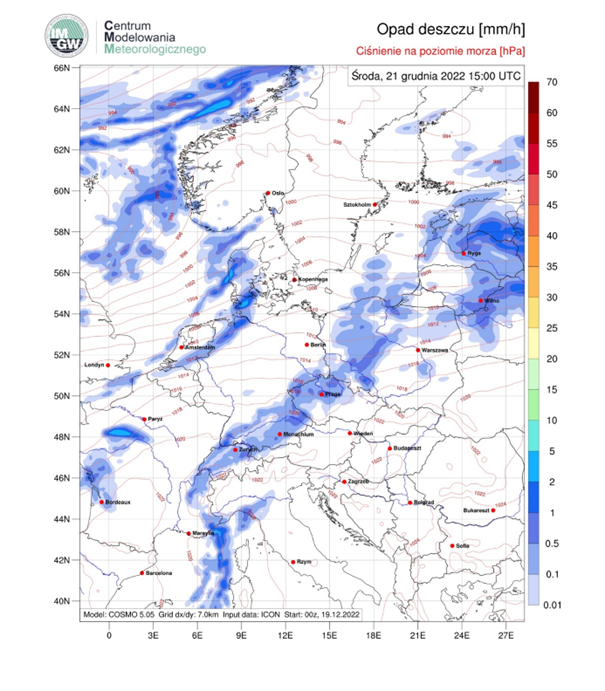
Opady: deszczu. Szczegółowy rozkład pola opadu na załączonej mapie prognostycznej.

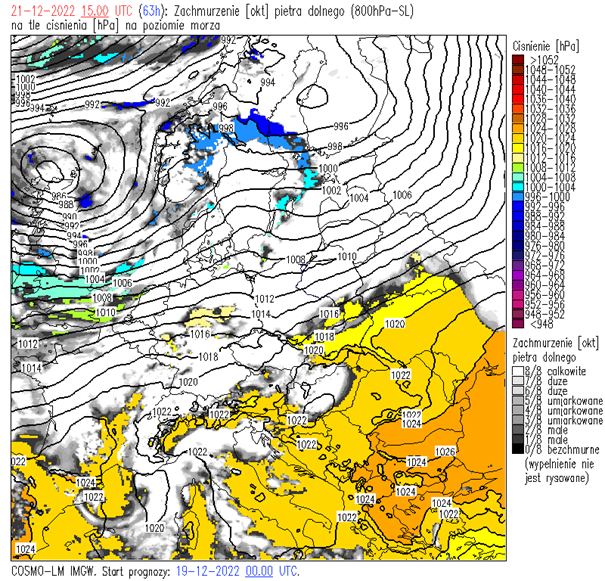
Zachmurzenie piętra niskiego: za wyjątkiem obszaru południowo-wschodniego zachmurzenie duże, na niebie Stratocumulus, Stratus fractus.

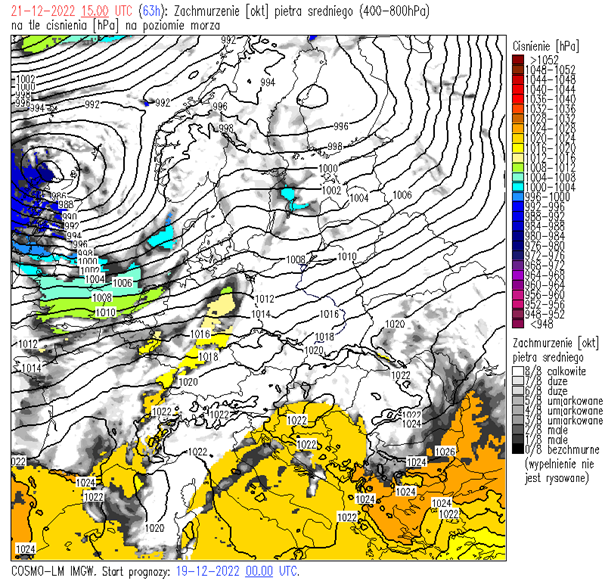
Zachmurzenie piętra średniego: całkowite, Altocumulus, Altostratus.

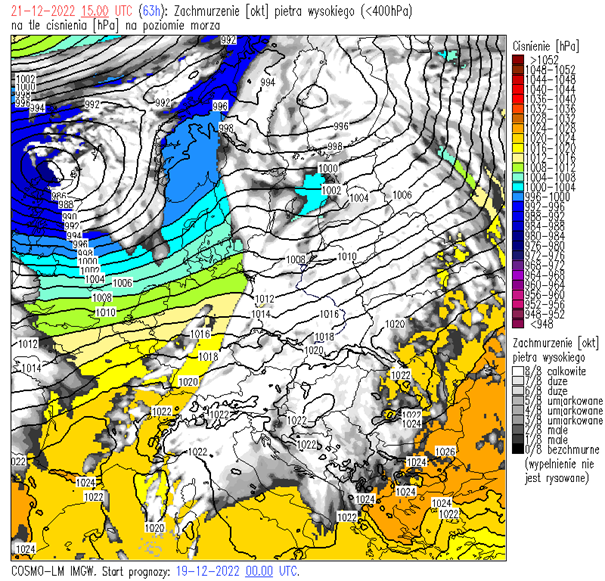
Zachmurzenie piętra wysokiego: całkowite. Na niebie Cirrus fibratus/spissatus, Cirrostratus fibratus.

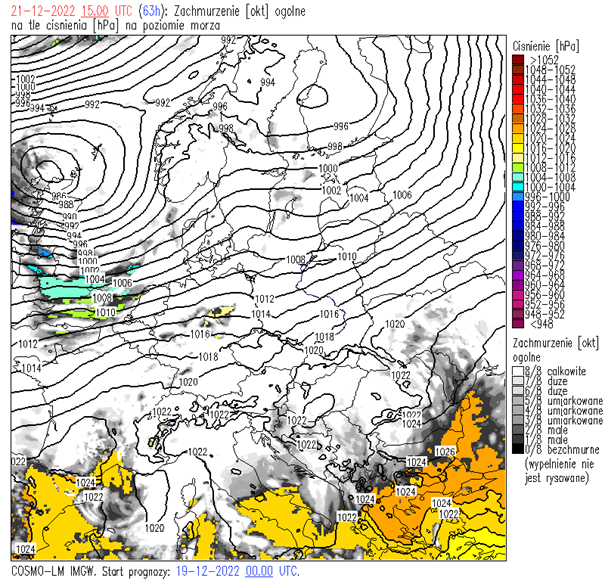
Zachmurzenie ogólne: całkowite.

Warunki obserwacyjne: brak dobrych warunków do obserwacji.

Opracowanie:

dr Grzegorz Duniec, Centrum Modelowania Meteorologicznego IMGW-PIB