Superksiężyc oraz rozmaitości o orbicie księżycowej

Opracowanie: dr Grzegorz Duniec, IMGW-PIB Centrum Modelowania Meteorologicznego

Przed nami dwie pełnie Księżyca które przypadną na czas, kiedy nasz naturalny satelita znajdzie się w pobliżu perygeum swojej orbity. Najbliższa pełnia wypada 31 sierpnia 2023 roku o godzinie 3³⁶. Księżyc przejdzie przez perygeum swojej orbity 30 sierpnia 2023 roku o godzinie 17⁵⁶.

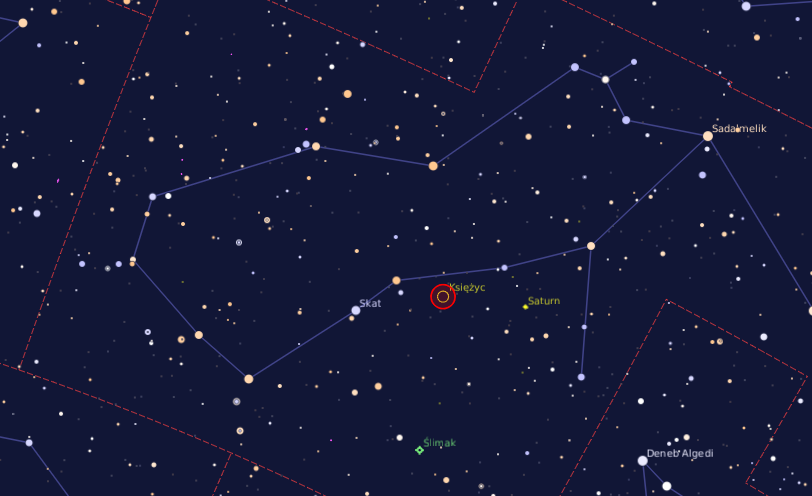
Wygląd nieba z dnia 31 sierpnia 2023 roku. Źródło: Program astronomiczny Periapsis, Autor: Bartosz Wojczyński, Wydawca: AstroCD – Sylwia Substyk

Księżyc znajdzie się w konstelacji Wodnika, w niedalekiej odległości od Saturna.

Kolejna pełnia przypada 29 września 2023 roku o godzinie 11⁵⁷. Natomiast Księżyc znajdzie się w perygeum swojej orbity 28 września 2023 roku o godzinie 3⁰¹.

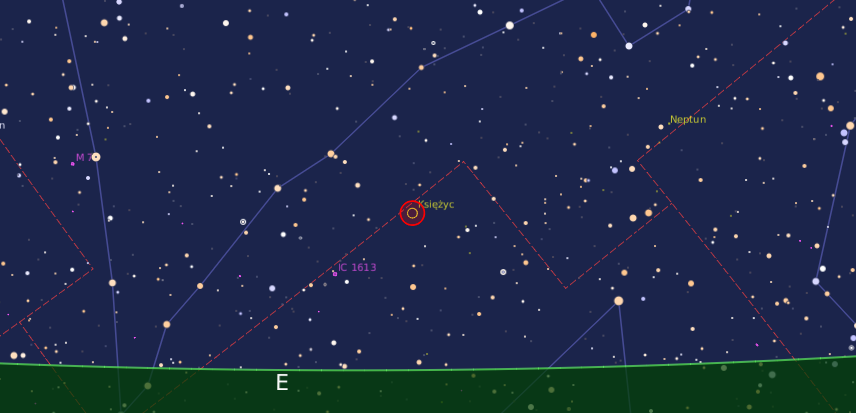
Wygląd nieba z dnia 29 września 2023 roku, o godzinie 19:37. Źródło: Program astronomiczny Periapsis, Autor: Bartosz Wojczyński, Wydawca: AstroCD – Sylwia Substyk

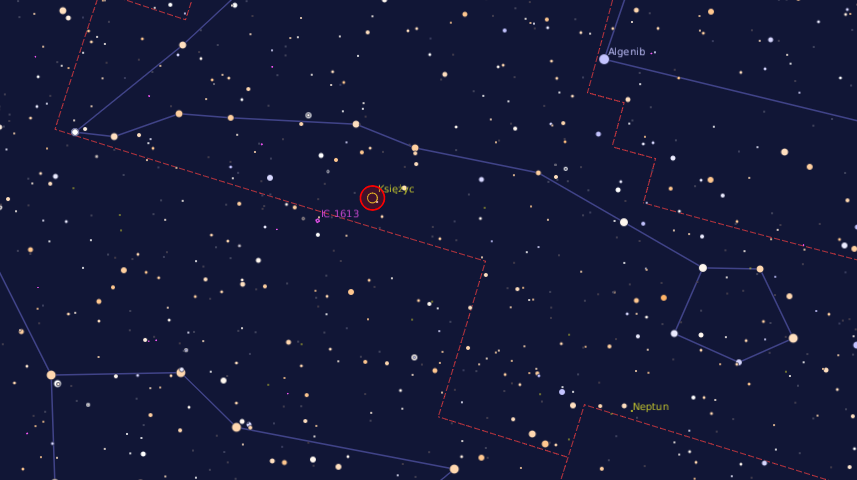
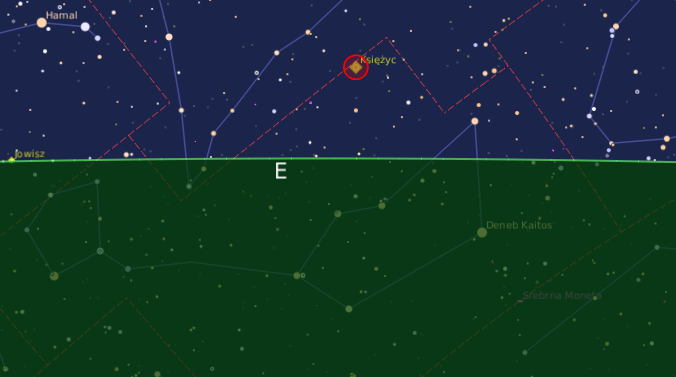
Wygląd nieba z dnia 30 września 2023 roku, godzina 2:37. Źródło: Program astronomiczny Periapsis, Autor: Bartosz Wojczyński, Wydawca: AstroCD – Sylwia Substyk

Początkowo Księżyc, tuż po wschodzie, będzie znajdował się jeszcze w obszarze gwiazdozbioru Wieloryba. Około godziny 21:16 Księżyc wkroczy do gwiazdozbioru Ryb.

Podstawowe informacje o Księżycu

Księżyc to naturalny satelita Ziemi, który obiega planetę w czasie 27 dni 07 godzin 43 minut i 11,51 sekundy. W rzeczywistości Księżyc obiega środek masy układu Ziemia-Księżyc, który znajduje się w odległości 4670 km od centrum planety [1]. Okres obiegu nazywamy miesiącem syderycznym, czyli miesiącem gwiazdowym. Miesiąc gwiazdowy to czas jaki jest potrzebny, aby Księżyc obiegając Ziemię po orbicie, przyjął taką samą pozycję na tle gwiazd. Księżyc obiega Ziemię po orbicie w przybliżeniu eliptycznej o średnim mimośrodzie wynoszącym 0,0549. Zatem przy średnim mimośrodzie Księżyc w perygeum zbliża się do Ziemi na odległość 363396 km, zaś w apogeum oddala się od Ziemi na odległość 405504 km [Meeus]. Czas jaki upływa między dwoma następującymi po sobie przejściami Księżyca przez perygeum średnio wynosi 27 dni 13 godzin 18 minut i 33 sekundy [2]. Okres ten nazywamy miesiącem anomalistycznym. Płaszczyzna orbity księżycowej jest nachylona do płaszczyzny ekliptyki pod kątem 5°08’43,4” [1]. Obie płaszczyzny przecinają się w dwóch punktach, które nazywamy węzłami orbity, wstępującym i zstępującym. Średni czas jaki upływa między dwoma przejściami Księżyca przez ten sam węzeł nazywamy miesiącem smoczym i wynosi 27 dni 05 godzin 05 minut 36 sekund [2]. Księżyc wykazuje fazy. Czas jaki upływa między dwiema tymi samymi fazami nazywamy miesiącem synodycznym i wynosi 29 dni 12 godzin 44 minuty 02,78 sekundy [1].

Powyżej scharakteryzowano ruch Księżyca wyodrębniając cykle zwane miesiącami i wskazano średnią długość poszczególnych miesięcy. Z naukowego punktu widzenia oraz czystej ciekawości nasuwa się pytanie, czy długość poszczególnych miesięcy jest stała, a jeśli nie to od czego ona zależy. Mechanika nieba zaspokoiła ludzką ciekawość.

Księżyc wzajemnie oddziałuje grawitacyjnie z Ziemią, ale także oddziałuje ze Słońcem oraz innymi planetami. Porównując wartości liczbowe oddziaływania grawitacyjnego spostrzec można, że Słońce oddziałuje prawie dwukrotnie silniej niż Ziemia. Oddziaływanie pozostałych planet, w tym Jowisza i Saturna jako największych planet w Układzie Słonecznym jest na tyle małe, że może zostać pominięte w pierwszym przybliżeniu. Zatem na ruch Księżyc w znacznym stopniu wpływa Słońce, które jest głównym ciałem zaburzającym orbitę księżycową. W wyniku oddziaływania Słońca orbita Księżyca nie jest idealną elipsą jakiej można by się było spodziewać, jak przy zagadnieniu dwóch ciał. Nasz przypadek należy potraktować jako zagadnienie trzech ciał, gdzie Słońce jest czynnikiem zaburzającym ruch naszego satelity. Zatem podane powyżej średnie czasy poszczególnych cykli będą się zmieniały. Przyjrzyjmy się im z bliska.

Miesiąc syderyczny, odległość Księżyca od Ziemi

Miesiąc syderyczny jest równy czasowi jaki potrzebuje Księżyc, aby dokonać jednego pełnego obiegu wokół Ziemi w średniej odległości 384402 km. Czas obiegu Księżyca zależy od jego odległości od ciała Ziemi. Zatem czy średnia odległość Księżyca od Ziemi jest stała? Jak wiadomo Słońce oraz Księżyc jest odpowiedzialne za zjawisko pływów na Ziemi. Kiedy poziom wody podnosi się wówczas obserwujemy przypływ, kiedy obniża wówczas występuje odpływ. Słońce jest o wiele większe od Księżyca, ale znajduje się daleko od Ziemi. Księżyc jest mały w porównaniu ze Słońce, ale znajduje się bliżej, skutkuje to tym, że siły pływowe ze strony Księżyca są większe niż ze strony Słońca. Prostym rachunkiem można udowodnić, że wartość siły przypływowej pochodzącej od Słońca jest 2,17 razy mniejsza niż wartość siły przypływowej księżycowej [3]. Jak podnoszenie się powierzchni wody jest skorelowane z położeniem ciała niebieskiego, np. Księżyca? W sytuacji idealnej należałoby oczekiwać, że w chwili kulminacji Księżyca, który przecina południk niebieski, również powinno się zaobserwować podniesienie powierzchni wody. Obserwacje jednak temu przeczą. Maksimum podniesienia powierzchni wody obserwuje się w chwili, kiedy Księżyc już jest po kulminacji. Przyczyny należy upatrywać w tarciu przypływowym, które jest kluczowe w wyjaśnieniu jak siły pływowe wpływają na orbitę księżycową [4]. W sytuacji idealnej, czyli bez tarcia pływowego, występuje sytuacja symetryczna, nie pojawia się żaden moment sił działający na Księżyc. Zatem jakikolwiek wpływ fali przypływowej ziemskiej na orbitę księżycową w wyniku uśrednienia wyzeruje się. W sytuacji występowania tarcia przypływowego, symetria nie występuje. Pojawia się moment sił działający na Ziemię oraz na Księżyc. Oba momenty sił są równe co do wartość, ale są przeciwnie skierowane. Moment sił działający na Ziemie skutkuje tym, że Ziemia zaczyna obracać się coraz wolniej. Moment sił działający na Księżyc wywołuje przyspieszenie w ruchu orbitalnym. Z punktu widzenia energetycznego energia mechaniczna układu Ziemia-Księżyc zmienia się. Energia kinetyczna układu częściowo ulega dyssypacji a częściowo zostaje zamieniona na energię kinetyczną i potencjalną ruchu Księżyca [4]. Przeprowadzając szczegółowe obliczenia można wykazać, że Księżyc oddala się średnio o 3,8 cm w ciągu roku [5]. Skoro Księżyc się oddala to i długość miesiąca syderycznego będzie się stopniowo wydłużała.

Nachylenie orbity księżycowej względem płaszczyzny ekliptyki

W wyniku oddziaływania Słońca, które zaburza ruch Księżyca, występują zmiany nachylenia orbity księżycowej względem płaszczyzny ekliptyki.

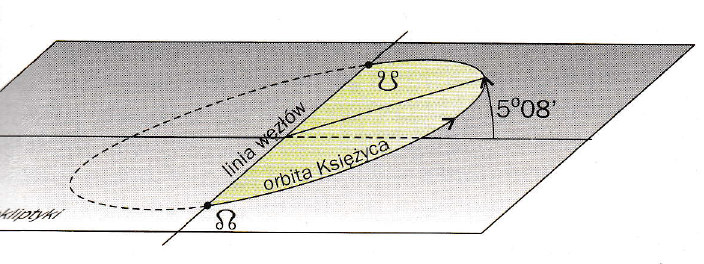
Rys 1. Eliptyczna orbita Księżyca i linia węzłów. Źródło: Jerzy M. Kreiner, Ziemia i Wszechświat – astronomia nie tylko dla geografów, Wydawnictwo Naukowe Uniwersytetu Pedagogicznego, Kraków, 2009.

Nachylenie zmienia się w granicach od 4°59’ do 5°19’ [1]. Okres zmian wynosi 173,3 dni [2,6]. Płaszczyzna orbity księżycowej przecina płaszczyznę ekliptyki. Punkty, w których płaszczyzna księżycowa przecina ekliptykę nazywamy węzłami księżycowymi, a linia łącząca oba węzły nazywamy linią węzłów. Jeżeli linia węzłów pokrywa się z linią łączącą Słońce i Ziemi, czyli różnica w długości ekliptycznej węzła wstępującego względem Słońca wynosi 0° i 180°, wówczas płaszczyzna orbity księżycowej jest nachylona pod kątem maksymalnym. A więc w czasie występowania okresu zaćmień Słońca lub Księżyca orbita jest nachylona pod największym kątem względem płaszczyzny ekliptyki. Kiedy linia węzłów jest prostopadła do linii łączącej Ziemię i Księżyc, czyli wtedy, kiedy różnica w długości ekliptycznej między węzłem wstępującym i Słońcem wynosi 90° lub 270° wówczas nachylenie płaszczyzny księżycowej będzie najmniejsza [2].

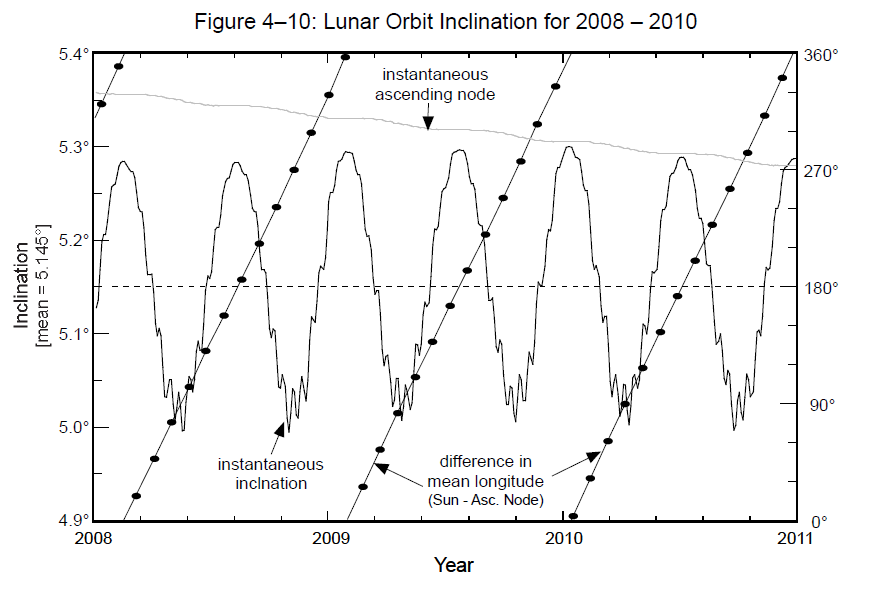
Rys 2. Zmiana nachylenia orbity księżycowej w funkcji czasu. Źródło: Fred Espenak, Jean Meeus, Five Millennium Catalog of Solar Eclipses: -1999 to +3000 (2000BCE to 3000 CE) – revised, NASA, January 2009, NASA/TP-2009-214174.

Ruch węzłów księżycowych, długość miesiąca smoczego

Węzły księżycowe poruszają ruchem retrogradacyjnym, czyli ruchem wstecznym. Rzeczywisty ruch węzłów nie jest jednostajny. Prędkość średnia z jaką cofają się węzły wynosi 0,05295°/dzień. Prędkość z jaką poruszają się węzły jest zmienna. Kiedy różnica w długości ekliptycznej Słońca i węzła wstępującego wynosi 0° lub 180° wówczas ich prędkość wynosi niemal zero. Węzły są niemal stacjonarne. Linia węzłów dokonuje jednego pełnego obrotu w czasie 6793,48 dni względem gwiazd oraz 6798,38 dni względem punktu równonocy wiosennej, czyli punktu Barana [6].

W związku z niejednostajnością ruchu węzłów księżycowych również długość miesiąca smoczego nie jest stała. Kiedy węzły zwalniają i poruszają się wolniej wówczas długość miesiąca smoczego wydłuża się osiągając maksimum, kiedy różnica w długości ekliptycznej Słońca i węzła wstępującego wyniesie 0° lub 180°. Kiedy prędkość węzłów zwiększa się wówczas długość miesiąca smoczego się skraca. Najkrótszy miesiąc smoczy występuje wówczas, kiedy różnica w długości ekliptycznej Słońca i węzła wstępującego wyniesie 90° lub 270°. Z powyższego wynika, że położenie węzła wstępującego względem Słońce wpływa na długość miesiąca smoczego. Okres zmian długości miesiąca smoczego wynosi 173,3 dnia [2,6].

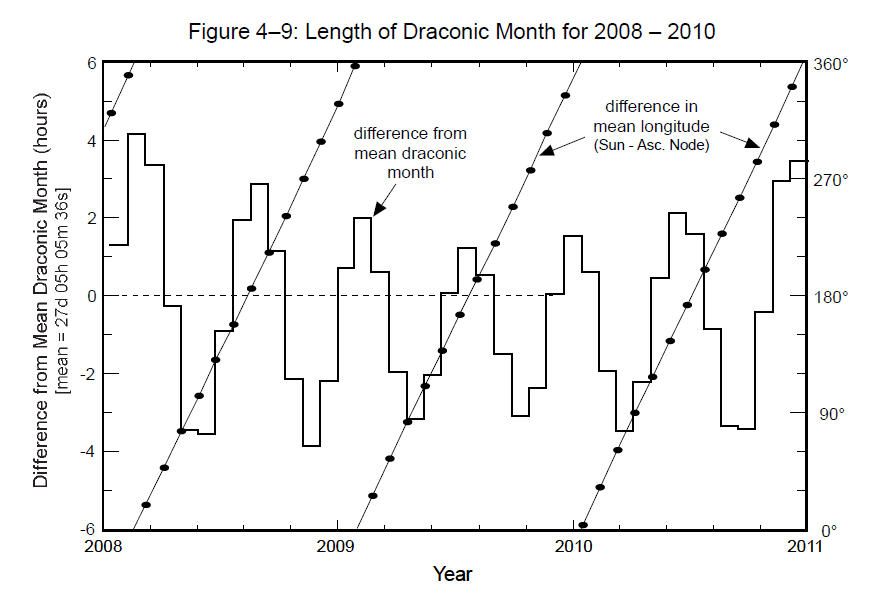
Rys. 3. Zmiana długości miesiąca smoczego w funkcji czasu. Źródło: Fred Espenak, Jean Meeus, Five Millennium Catalog of Solar Eclipses: -1999 to +3000 (2000BCE to 3000 CE) – revised, NASA, January 2009, NASA/TP-2009-214174.

Ale czy tylko? Mechanika nieba daje odpowiedź na to pytanie. Okazuje się, że położenie perygeum względem węzła wstępującego również wpływa na długość miesiąca smoczego. Kiedy perygeum orbity wypada w węźle wstępującym wówczas długość miesiąca synodycznego będzie najdłuższa. Kiedy perygeum orbity wypadnie w węźle zstępującym wówczas długość miesiąca smoczego będzie najkrótsza. Jaki jest okres powyższych zmian. Otóż jak wiadomo, oś węzłów zakreśla w kierunku wstecznym kąt o wartości 0,05295° dziennie. Linia apsyd, czyli linia łącząca punkt perygeum i apogeum zakreśla w przestrzeni kąt 0,11140° dziennie w ruchu prostym [2]. Czas jaki upływa pomiędzy kolejnymi następującymi po sobie zdarzeniami polegającymi na tym, że perygeum wypada w węźle wstępującym wynosi 2190,4 dnia, czyli 6 lat.

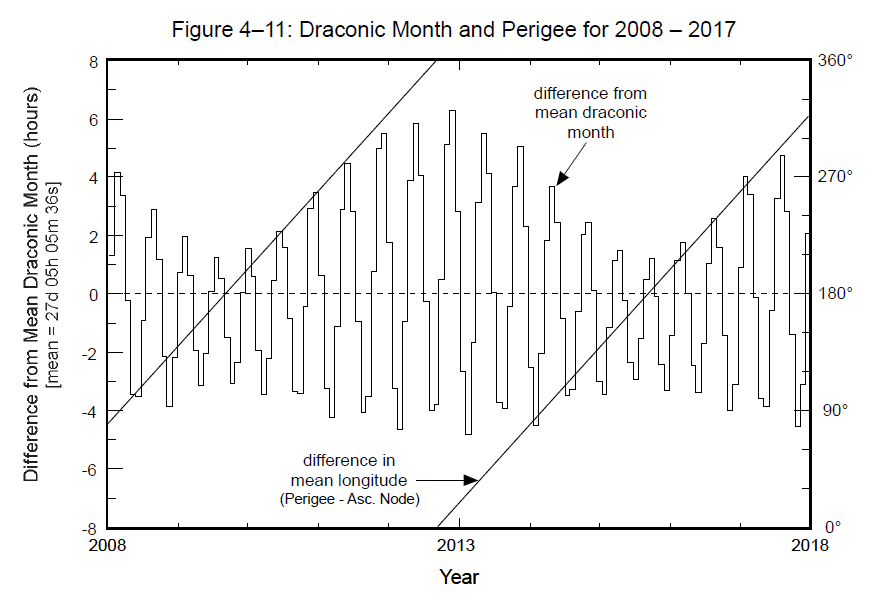
Rys. 4. Zmiana długości miesiąca księżycowego w funkcji czasu i różnicy ekliptycznej perygeum i węzła wstępującego Księżyca. Źródło: Fred Espenak, Jean Meeus, Five Millennium Catalog of Solar Eclipses: -1999 to +3000 (2000BCE to 3000 CE) – revised, NASA, January 2009, NASA/TP-2009-214174.

Z symulacji numerycznych wykonanych przez Jeana Meeusa, obejmujących 5000 lat wynika, że najkrótszy miesiąc synodyczny wynosił 27 dni 5 minut 45,6 sekund (27,004 dnia). Najdłuższy miesiąc synodyczny wynosił 27 dni 11 godzin 41 minut 16,8 sekund (27,487 dnia) [2].

Mimośród orbity Księżyca

Księżyc w przybliżeniu porusza się po orbicie w przybliżeniu eliptycznej o średnim mimośrodzie 0,0549. Poruszając się po orbicie eliptycznej Księżyc zbliża się i w perygeum orbity odległość będzie najmniejsza. Kiedy Księżyc oddala się w apogeum orbity osiąga największą odległość od Ziemi. W wyniku zaburzenia orbity Księżycowej przez Słońce mimośród zmienia się, co pociąga za sobą zmianę najmniejszej i największej odległość od Ziemi. Linia apsyd to linia łącząca perygeum i apogeum orbity. Kiedy linia apsyd pokrywa się z kierunkiem łączącym Ziemię i Słońce (różnica w długości ekliptycznej perygeum orbity i Słońca wyniesie 0° oraz 180°) wówczas oddziaływanie grawitacyjne Słońca powoduje, że mimośród orbity wzrasta, orbita jest bardziej eliptyczna. Kiedy linia apsyd usytuowana jest w kierunku prostopadłym względem kierunku do Słońca (różnica w długości ekliptycznej perygeum orbity i Słońca wyniesie 90° oraz 270°) wówczas mimośród orbity osiąga minimum. Orbita staje się bardziej kolista. Czas jaki upływa między dwoma ekstremalnymi wartościami mimośrodu wynosi 205,9 dnia [2,6].

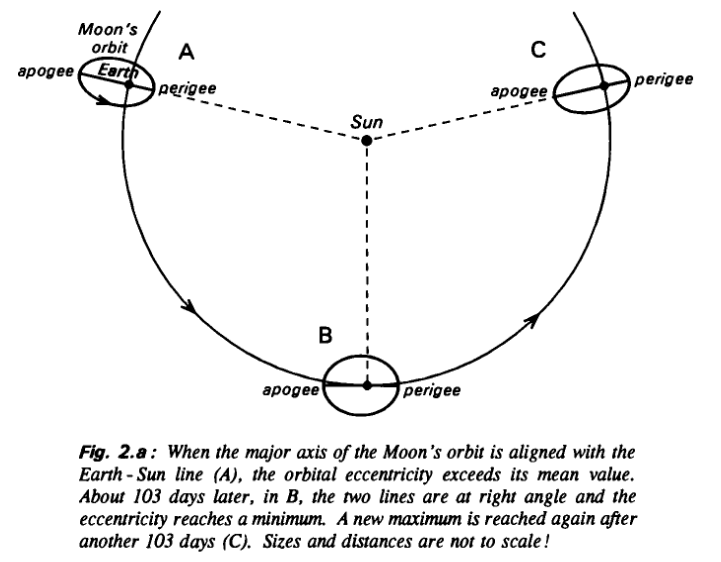
Rys. 5. Zmiana mimośrodu orbity księżycowej. Żródło: Jean Meeus, Mathematical Astronomy Morsels, Willmann-Bell, Inc, 1997.

Z symulacji numerycznych obejmujących 5000 lat wynika, że ekstremalne wartości mimośrodu wahają się w granicach od 0,0255 do 0,0775 [2].

Długość miesiąca anomalistycznego

Miesiąc anomalistyczny jest to czas jaki upływa między dwoma przejściami Księżyca przez perygeum. Średnia długość miesiąca anomalistycznego wynosi 27 dni 13 godzin 18 minut 33 sekund. Długość miesiąca anomalistycznego jest nieco dłuższy od miesiąca syderycznego. Przyczyny należy upatrywać w tym, że linia apsyd nie zajmuje stałego położenia. W przestrzeni linia apsyd zakreśla 0,11140° dziennie w kierunku prostym i zakreśla pełen okręg w czasie 3232,61 dnia względem gwiazd i 3231,5 dnia względem punktu Barana (tzw. okres tropikalny) [2,6].

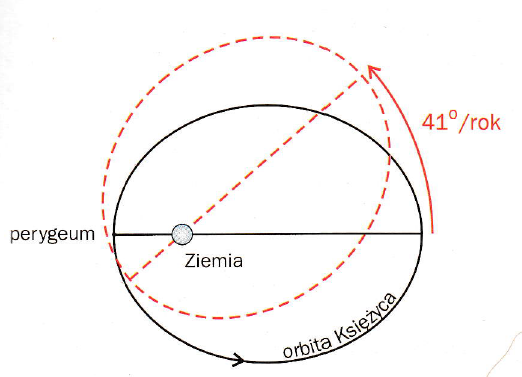
Rys. 6. Miesiąc anomalistyczny. Źródło: Jerzy M. Kreiner, Ziemia i Wszechświat – astronomia nie tylko dla geografów, Wydawnictwo Naukowe Uniwersytetu Pedagogicznego, Kraków, 2009.

Długość miesiąca anomalistycznego zależy od położenia linii apsyd orbity księżycowej względem Słońca. Kiedy linia apsyd skierowana jest w kierunku Słońca (różnica w długości ekliptycznej perygeum i Słońca wynosi 0° i 180°) wówczas długość miesiąca anomalistycznego będzie najdłuższa. Kiedy linia apsyd jest prostopadła w stosunku do kierunku Słońca (różnica w długości ekliptycznej perygeum i Słońca wynosi 90° i 270°) wówczas długość miesiąca będzie najkrótsza. Z obliczeń wynika, że czas jaki upływa między dwoma następującymi przejściami Księżyca przez perygeum orbity waha się od 24 dni i 16 godzin do 28 dni i 13 godzin. Natomiast czas jaki upływa między dwoma następującymi po sobie przejściami przez apogeum waha się od 26 dni 23 godzin 31 minut i 12 sekund do 27 dni 21 godzin 36 minut [7].

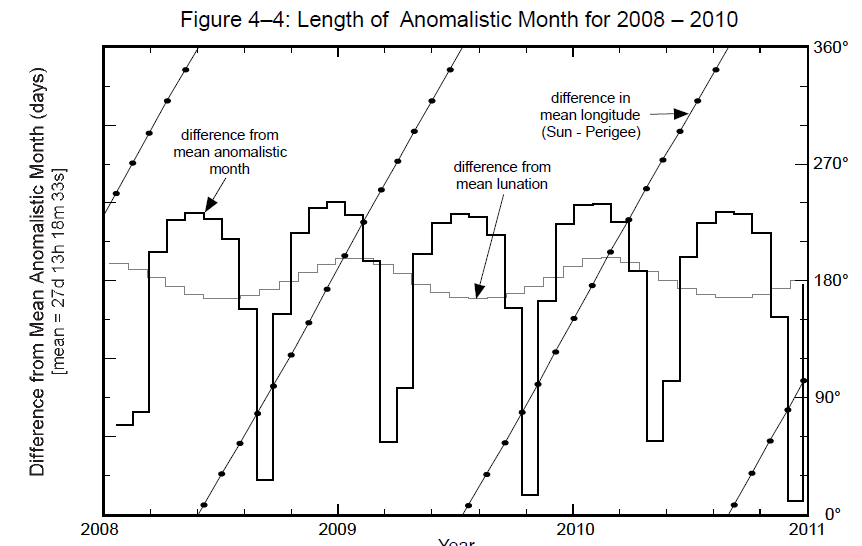
Rys. 7. Długość miesiąca anomalistycznego w funkcji czasu. Źródło: Fred Espenak, Jean Meeus, Five Millennium Catalog of Solar Eclipses: -1999 to +3000 (2000BCE to 3000 CE) – revised, NASA, January 2009, NASA/TP-2009-214174.

Fazy Księżyca, miesiąc synodyczny

Od kiedy tylko rozumie spojrzymy na Księżyc prędzej czy później zauważamy, że Księżyc wykazuje fazy.

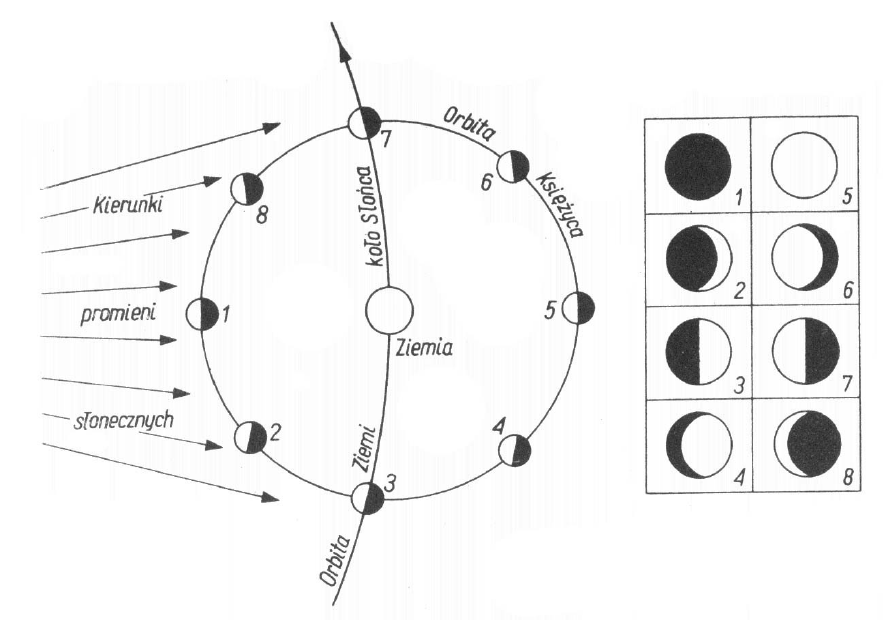
Rys. 8. Fazy Księżyca. Źródło: Konrad Rudnicki, Astronomia dla kl. IV liceum ogólnokształcącego, technikum i liceum zawodowego, wyd. XV, WSiP, 1988.

Średni odstęp czasu jaki upływa między dwoma takimi samymi lunacjami nazywamy miesiącem synodycznym i wynosi 29 dni 12 godzin 44 minut 02,78 sekund [1]. Gdyby Ziemia spoczywała wówczas długość miesiąca synodycznego i syderycznego byłaby taka sama. Ale Ziemia się porusza na orbicie wokół Słońca. Po upływie miesiąca gwiazdowego, kiedy Księżyc wykona jeden pełen obieg wokół Ziemi, znajdzie się wówczas na tle tych samych gwiazd (przy założeniu braku perturbacji orbity). Ale czy Księżyc będzie w tej samej fazie? Otóż nie. Jeżeli rozpoczęlibyśmy obserwację Księżyca będącego w fazie nowiu to po upływie miesiąca gwiazdowego, kiedy spojrzymy w niebo, spostrzeżemy Księżyc, który będzie w fazie sierpa malejącego. Ze względu na ruch obiegowy Ziemi, potrzebny jest dodatkowy czas, w trakcie którego długość ekliptyczna Słońca i Księżyca zrówna się, a dla obserwatora ziemskiego Księżyc będzie w nowiu.

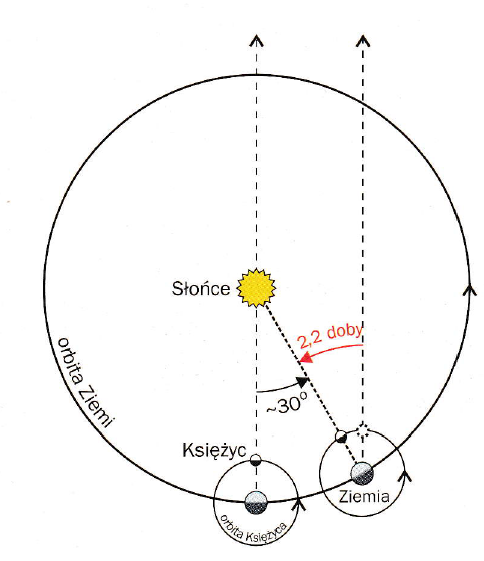
Rys. 9. Miesiąc synodyczny i miesiąc gwiazdowy. Źródło: Jerzy M. Kreiner, Ziemia i Wszechświat – astronomia nie tylko dla geografów, Wydawnictwo Naukowe Uniwersytetu Pedagogicznego, Kraków, 2009.

Dociekliwy obserwator zada pytanie, czy długość miesiąca synodycznego jest stała? Mechanika nieba jak i doświadczenie obserwatora udziela odpowiedzi twierdzącej, że nie jest stała. Okazuje się, że kiedy Ziemia zbliża się do peryhelium orbity wówczas na orbicie porusza się coraz szybciej. Księżyc po wykonaniu jednego pełnego obiegu wokół Ziemi, musi zakreślać coraz większy dodatkowy łuk, aby ponownie znalazł się w tej samej fazie. Zatem kiedy Ziemia znajduje się w peryhelium orbity długość miesiąca synodycznego jest najdłuższa. Latem, kiedy Ziemia zbliża się do aphelium swojej orbity, Ziemia zaczyna się poruszać coraz wolniej. Zatem długość miesiąca synodycznego skraca się. Zatem kiedy Ziemia znajdzie się w aphelium orbity długość miesiąca synodycznego jest najkrótsza [2]. Długość cyklu wynosi w przybliżeniu rok. Ale czy tylko eliptyczność orbity ziemskiej wpływa na długość lunacji? Otóż nie. Rozpocznijmy rozważania od sytuacji, kiedy nów Księżyca przypada na okres, kiedy Księżyc znajduje się w perygeum orbity. Kiedy upłynie miesiąc anomalistyczny, czyli kiedy ponownie Księżyc znajdzie się w perygeum orbity to czy Księżyc znajdzie się nowiu? Nie, Księżyc będzie w fazie sierpa malejącego. Musi w przestrzeni zakreślić dodatkowy łuk o długości Δb. Po upływie około 206 dni nów Księżyca przypadnie na czas, kiedy Księżyc znajduje się w apogeum. Kiedy Księżyc ponownie znajdzie się w apogeum swojej orbity, jak się domyślamy, będzie fazie sierpa ubywającego. Aby ponownie był w fazie nowiu, musi zakreślić dodatkowy łuk o długości Δd. Nasuwa się naturalne pytanie, czy długość obu łuków będzie równej długości? Kiedy Księżyc znajduje się w perygeum orbity porusza się szybciej, ale również jest najbliżej Ziemi. W apogeum Księżyc porusza się wolniej a jego odległość od Ziemi największa. Zatem Księżyc w perygeum musi zakreślić krótszy łuk w porównaniem z łukiem zakreślanym, kiedy znajduje się w apogeum, aby znaleźć się ponownie w fazie nowiu, Δb < Δd [2]. Zatem długość miesiąca synodycznego jest dłuższa od średniej długości, kiedy nów wypada w apogeum, a krótsza od średniej długości, kiedy nów Księżyca wypada w perygeum. Długość cyklu wynosi 412 dni. Z przeprowadzonych obliczeń przez Jeana Meeusa, który obejmował okres 5000 lat, najkrótszy miesiąc synodyczny wynosił 29 dni 6 godzin 22 minuty 40 sekund. Najdłuższy zaś miał długość 29 dni 20 godzin 10 minut 53 sekundy.

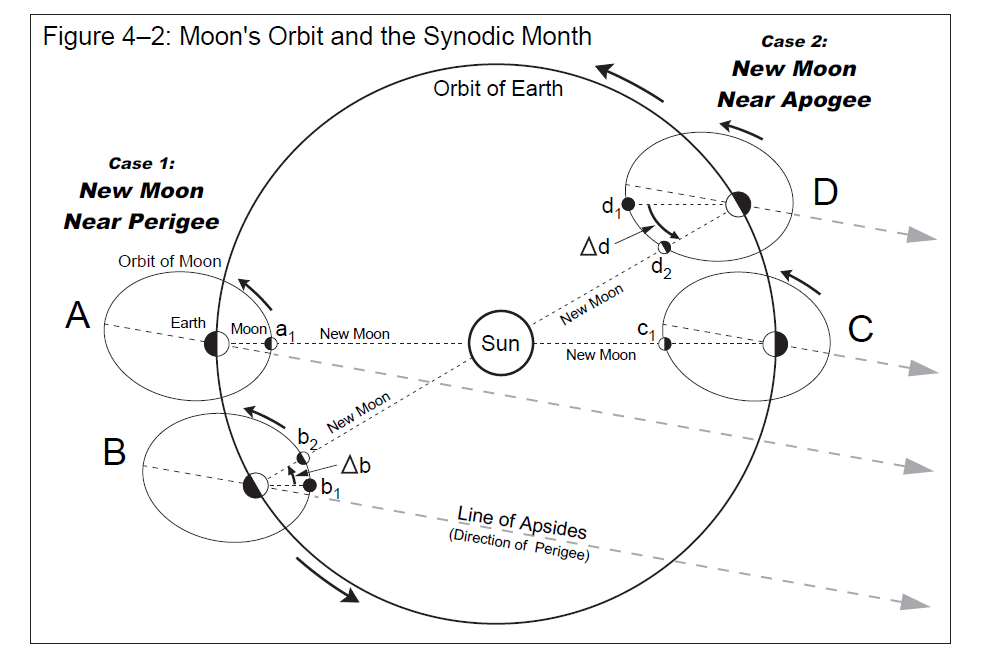
Rys. 10. Długość miesiąca synodycznego w kontekście orbity księżycowej. Żródło: Fred Espenak, Jean Meeus, Five Millennium Catalog of Solar Eclipses: -1999 to +3000 (2000BCE to 3000 CE) – revised, NASA, January 2009, NASA/TP-2009-214174.

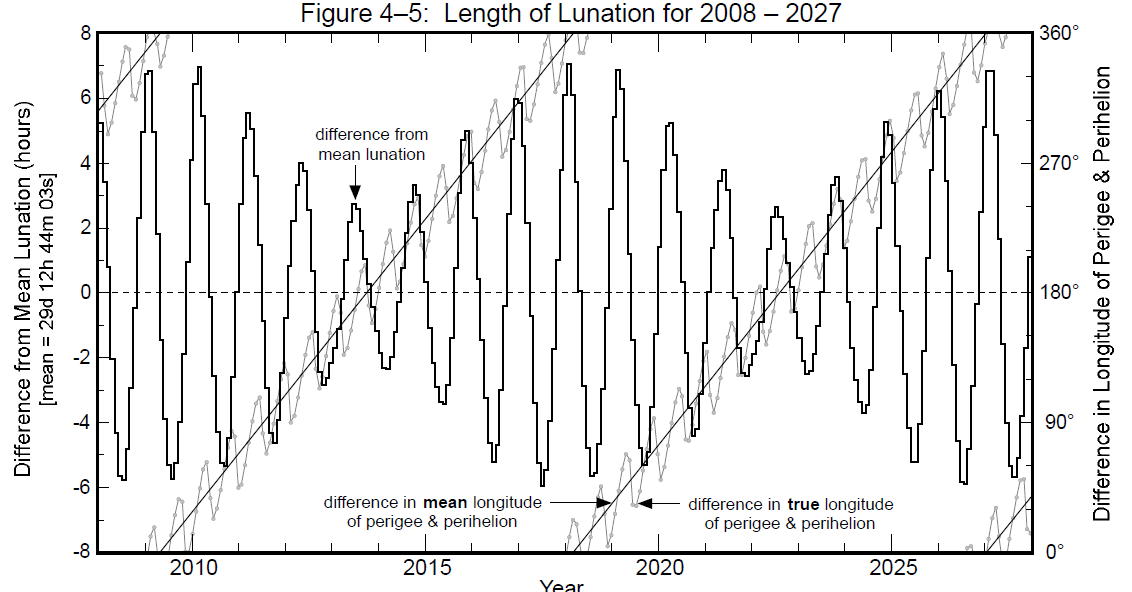
Rys. 11. Długość lunacji księżycowej w funkcji czasu. Żródło: Fred Espenak, Jean Meeus, Five Millennium Catalog of Solar Eclipses: -1999 to +3000 (2000BCE to 3000 CE) – revised, NASA, January 2009, NASA/TP-2009-214174.

Obserwacje również potwierdzają, że na długość miesiąca synodycznego (co jest właściwie oczywistością wynikającą z powyższych rozważań) wpływa także wzajemnie położenie linii apsyd orbity księżycowej oraz ziemskiej. Kiedy różnica długości ekliptycznych wynosi 0°, czyli wówczas, kiedy linie są równolegle i pokrywają się perygeum i peryhelium, wówczas długość miesiąca synodycznego jest najdłuższa. Natomiast kiedy linie apsyd się pokrywają, ale różnica w długości ekliptycznej perygeum i peryhelium wynosi 180° wówczas długość miesiąca synodycznego jest najkrótsza. Ile trwa cykl zmian? Jak wspomniano wyżej linia apsyd orbity Księżycowej zakreśla łuk 0,1114° dziennie i zakreśla ona łuk 360° w czasie 8,85 roku. Linia apsyd orbity Ziemskiej zakreśla łuk znacznie mniejszy 0,0172° rocznie, zakreślając pełny łuk 360° w ciągu 20500 lat. Zatem czas jaki upłynie między ponownym równoległym ustawieniem linii apsyd (ponownie długości ekliptyczne peryhelium i perygeum będą sobie równe) wynosi 3232,61 dnia. Zatem długość cyklu zmian w długości miesiąca synodycznego wynikającego ze wzajemnego położenia orbit ziemskiej i księżycowej wynosi 3232,61 dnia. Z obliczeń wynika, że długość miesiąca synodycznego (wtedy, kiedy długości ekliptyczne peryhelium i perygeum będą sobie równe) waha się od minimum wynoszącego 29,273 dnia (29 dni 6 godzin 33 minuty 7,2 sekund) do maksimum wynoszącego 29,820 dnia (29 dni 19 godzin 40 minuty 48 sekund). Natomiast długość miesiąca synodycznego (wtedy, kiedy długości ekliptyczne peryhelium i perygeum będą różniły się o 180°) waha się od minimum wynoszącego 29,452 dnia (29 dni 10 godzin 50 minuty 52,8 sekund) do maksimum wynoszącego 29,628 dnia (29 dni 15 godzin 04 minuty 19,2 sekund) [2].

Rozważmy długość lunacji dla poszczególnych faz księżyca [8].

Nów Księżyca:

Najkrótszy okres lunacji: 29 dni 6 godzin 34 minuty;

Najdłuższy okres lunacji: 29 dni 19 godzin 58 minut.

Pełnia Księżyca:

Najkrótszy okres lunacji: 29 dni 6 godzin 34 minuty;

Najdłuższy okres lunacji: 29 dni 19 godzin 58 minut.

Pierwsza kwadra Księżyca:

Najkrótszy okres lunacji: 29 dni 4 godzin 13 minuty;

Najdłuższy okres lunacji: 29 dni 22 godzin 15 minut.

Trzecia kwadra Księżyca:

Najkrótszy okres lunacji: 29 dni 4 godzin 14 minuty;

Najdłuższy okres lunacji: 29 dni 22 godzin 13 minut.

Dla faz pośrednich.

I oktant (45° od Słońca) – faza sierpa wzrastającego

Najdłuższy okres lunacji: 29 dni 21 godzin 12 minut.

III oktant (225° od Słońca) – faza Księżyca garbatego ubywającego

Najkrótszy okres lunacji: 29 dni 5 godzin 14 minuty;

Rozmiary kątowe Księżyca na sferze niebieskiej

Księżyc obiega Ziemie po orbicie w przybliżeniu eliptycznej. Obserwując ruch Księżyc na sferze niebieskiej spostrzeżemy, że jego rozmiary kątowe zmieniają się. Przy średniej odległości 384402 km średnica kątowa Księżyca wynosi 31’04,11”. Przy orbicie o mimośrodzie 0,0549 Księżyc w perygeum zbliży się do Ziemi na odległość 363298,3 km, wówczas jego rozmiary kątowe wyniosą 32’52,38”. W apogeum Księżyc oddala się od Ziemi na odległość 405505,7 km, wówczas średnica kątowa na sferze niebieskiej wyniesie 29’ 27,08”.

Przy zmniejszeniu sie mimośrodu orbity zakres zmian kątowych będzie mniejsza. Kiedy mimośród orbity wyniesie 0,0255 Księżyc w perygeum zbliża się do Ziemi na odległość 374599,7 km, zaś w apogeum Księżyc oddala się od Ziemi na odległość 394204,3 km. Rozmiary kątowe Księżyca zmieniają się od 31’52,87” w perygeum do 30’17,74” w apogeum.

Przy ekstremalnym mimośrodzie orbity wynoszącym 0,0775 odległość Księżyca w perygeum wyniesie 354610,8 km w perygeum, zaś w apogeum Księżyc oddala się od Ziemi na odległość 414193,2 km. Przy takim mimośrodzie rozmiary kątowe Księżyca zmieniają się od 33’40,7” w perygeum do 28’50,02” w apogeum.

Rozmiary i jasność Superksiężyca

Zjawisko Superksiężyca zachodzi wtedy, kiedy pełnia Księżyca znajduje się w pobliżu perygeum orbity. Rozważmy o ile Księżyc jest większy będąc w perygeum w stosunku do rozmiarów Księżyca znajdującego się w apogeum.

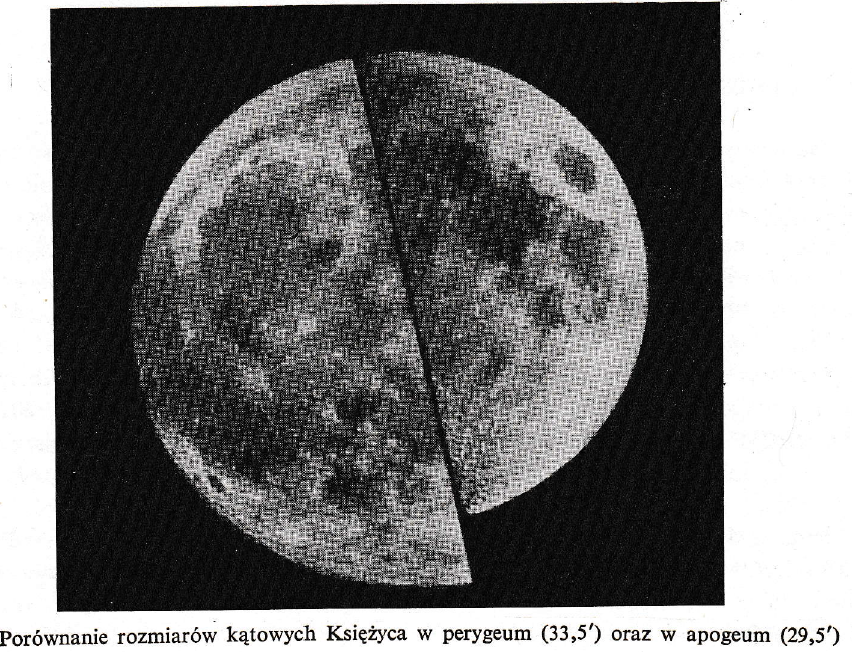
Rys. 12. Rozmiary kątowe Księżyca. Źródło: Jerzy Kreiner, Astronomia z astrofizyką, Wydawnictwo Naukowe PWN, 1992.

 

Przy średnim mimośrodzie (0,0549) Księżyc w perygeum jest o około 11,62 % większy od rozmiarów Księżyca znajdującego w apogeum.

Przy mimośrodzie najmniejszym i wynoszącym 0,0255 rozmiary kątowe Księżyca w perygeum są większe od rozmiarów kątowym Księżyca w apogeum o około 5,23 %.

Przy mimośrodzie ekstremalnie dużym wynoszącym 0,0775 Księżyc będzie większy nawet o 16,8% większy od rozmiarów Księżyca znajdującego się w apogeum.

Z czystej ciekawości przeliczmy, jak zmieniać się będą rozmiary kątowe Księżyca wraz ze zwiększaniem mimośrodu, w stosunku do rozmiarów kątowych Księżyca znajdującego się w średniej odległości.

Dla mimośrodu 0,0255, Księżyc w perygeum będzie większy o 2,6% od rozmiarów kątowych Księżyca znajdującego się w średniej odległości od Ziemi.

Dla mimośrodu 0,0549, Księżyc w perygeum będzie większy o 5,8% od rozmiarów kątowych Księżyca znajdującego się w średniej odległości od Ziemi.

Dla mimośrodu 0,0775, Księżyc w perygeum będzie większy o 8,4% od rozmiarów kątowych Księżyca znajdującego się w średniej odległości od Ziemi.

Zatem rozmiary Superksiężyca w pełni są na ogół większe od rozmiarów Księżyca w pełni przypadającej na położenie Księżyca inne niż perygeum, a więc wtedy, kiedy Księżyc nie jest najbliżej Ziemi.

Z elementarnych praw fizyki można oszacować, jak zmienia się natężenie oświetlenia powierzchni światłem Księżyca. Różnica natężenia oświetlenia między położeniem Księżyca w perygeum i apogeum, podczas pełni, dla mimośrodu 0,0255 wyniesie 10,7 %. Dla mimośrodu 0,0549 różnica w natężeniu oświetlenia wyniesie 24,6 %. Przy ekstremalnie dużym mimośrodzie orbity (0,0775) różnica w natężeniu oświetlenia wyniesie 36,4 %.

Czy wpływ eliptyczności orbity ziemskiej wpłynie na natężenie oświetlenia? Tak, ale zmiany te są znikomo małe w pierwszym przybliżeniu pomijalne.

Zatem czego możemy spodziewać się podczas Superksiężyca na niebie? Należy oczekiwać zwiększonego natężenia oświetlenia oraz większych rozmiarów Księżyca na sferze niebieskiej. Dla jednych obserwatorów będzie to piękne romantyczne wydarzenie. Inni będą cierpieć na bezsenność.

Literatura

1. Zbigniew Dworak, Z astronomią za pan brat, Iskry, Warszawa, 1989.
2. Fred Espenak, Jean Meeus, Five Millennium Catalog of Solar Eclipses: -1999 to +3000 (2000BCE to 3000 CE) – revised, NASA, January 2009, NASA/TP-2009-214174.
3. Jerzy M. Kreiner, Ziemia i Wszechświat – astronomia nie tylko dla geografów, Wydawnictwo Naukowe Uniwersytetu Pedagogicznego, Kraków, 2009.
4. Andrzej Kajetan Wróblewski, Janusz Andrzej Zakrzewski, Wstęp do fizyki, tom 2, część 1, PWN, 1989.
5. Frank D. Stacey and Paul M. Davis, Physics of the Earth, Fourth Edition, Cambridge University Press, 2013.
6. Jean Meeus, Mathematical Astronomy Morsels, Willmann-Bell, Inc, 1997.
7. Jean Meeus, Astronomical algorithms, Second English Edition, Willmann-Bell, Inc, 1998.
8. Jean Meeus, Mathematical Astronomy Morsels V, Willmann-Bell, Inc, 2009.
9. Konrad Rudnicki, Astronomia dla kl. IV liceum ogólnokształcącego, technikum i liceum zawodowego, wyd. XV, WSiP, 1988.
10. Jerzy Kreiner, Astronomia z astrofizyką, Wydawnictwo Naukowe PWN, 1992.

---

Udostępnij