Maksimum libracyjne Księżyca

Opracowanie: dr Grzegorze Duniec, dr Marcin Kolonko, IMGW-PIB CMM.

   Księżyc w wyniku działania sił przypływowych już dawno osiągnął rotację synchroniczną [1,2]. Naszą planetę czeka podobny efekt w przyszłości [3,4]. W wyniku rotacji synchronicznej Księżyc zawsze jest zwrócony do obserwatora ziemskiego tę samą stroną (ze względu na to, że ruch obrotowy Księżyca wokół własnej osi odbywa się w tym samym kierunku orbitalnym). Z takim zjawiskiem mamy do czynienia wtedy, kiedy okres obiegu Księżyca wokół Ziemi jest zrównany z okresem obrotu Księżyca wokół własnej osi. Jest to tzw. rotacja związana (lub inaczej synchroniczna). Na pierwszy rzut oka można odnieść wrażenie, że obserwator widzi dokładnie 50 % jego powierzchni (a dokładniej nieco mniej, ze względu na niewielką odległość od Ziemi) Czy tak jest w rzeczywistości?

   Rozpocznijmy analizę od założenia polegającego na tym, że ruch obiegowy Księżyca wokół Ziemi odbywać się będzie po orbicie kolistej oraz niech oś obrotu Księżyca będzie prostopadła do płaszczyzny jego orbity. Dzięki drugiemu założeniu, żaden punkt na powierzchni Księżyca nie będzie wykonywał pozornych ruchów względem obserwatora w kierunku północnym lub południowym podczas obiegu wokół Ziemi. Przeanalizujmy pozorny ruch wybranego punktu na powierzchni Księżyca (np. niech to będzie środek, czyli punkt o współrzędnych 0° szerokości i długości selenograficznej). Przy założeniu kołowej orbity prędkość kątowa Księżyca poruszającego się po orbicie jest identyczna z prędkością kątową jego obrotu wokół własnej osi. Zatem punkt wybrany przez obserwatora na powierzchni Księżyca nie będzie zmieniał swojego położenia względem obserwatora ziemskiego, podobnie z pozostałymi punktami na jego powierzchni. Obserwator z Ziemi obserwować będzie prawie 50 % jego powierzchni. Jak doskonale wszystkim wiadomo, postawione założenia nie są prawdziwe. Ze względu na eliptyczność orbity oraz braku prostopadłości osi obrotu do płaszczyzny jego orbity prosta łącząca środek Księżyca i Słońca nie przechodzi przez ten sam punkt na jego powierzchni tak jak to by było przy wyżej postawionych założeń. Człowiek obserwujący Księżyc w powierzchni Ziemi odnosi wrażenie jakby Księżyc kołysał się względem tej prostej (wahał się). Nazwa zjawiska libracji pochodzi od łacińskiego słowa libra – waga. W wyniku powyższego zjawiska obserwator ziemski ma możliwość zaobserwowania 59 % jego powierzchni. Zastanówmy się, dlaczego tak się dzieje.

   Teoria ruchu Księżyca wokół Ziemi została opracowana w 1693 roku przez Giovanniego Domenico Cassiniego (którego imieniem nazwano przerwę w pierścieniach Saturna oraz sondę kosmiczną) a jego spostrzeżenia zostały wyrażone w trzech empirycznych prawach [5,6]:

I prawo Cassiniego

Księżyc obraca się ruchem jednostajnym wokół stałej osi, przy czym czas jednego pełnego obrotu wynosi 27,321666 dnia.

II prawo Cassiniego

Nachylenie osi obrotu Księżyca do płaszczyzny jego orbity pozostaje stałe i wynosi 83°18’.

III prawo Cassiniego

Oś obrotu Księżyca, oś ekliptyki oraz oś orbity Księżyca leżą w jednej płaszczyźnie.

   Z III prawa wynika, że przecięcie płaszczyzny równika księżycowego, płaszczyzny orbity Księżycowej z płaszczyzną ekliptyki przecinają się z linią węzłów. Węzeł zstępujący równika księżycowego jest zbieżny z węzłem wstępującym orbity księżycowej. Z powyższego prawa empirycznego wynika jeszcze to, że precesja osi księżycowej zbiega się z okresem jednego pełnego obrotu węzłów księżycowych (6798,38 dni względem punktu równonocy wiosennej lub 6793,48 dni względem gwiazd) [6].

   Powyższe empiryczne prawa (opublikowany przez syna Cassiniego w 1721 r.) tłumaczą efekty libracyjne Księżyca. Wyróżnia się cztery rodzaje libracji: w długości, w szerokości oraz paralaktyczna zwana też dobową. Te trzy wymienione rodzaje libracji należą do tzw. libracji geometrycznych czy też inaczej nazywanych optycznych. Czwartym rodzajem libracji jest libracja fizyczna.

Libracje w długości

   Pierwszy rodzaj libracji w długości wynikają wprost z pierwszego prawa Cassiniego. Libracja w długości została odkryta przez Heweliusza w 1654 roku. Księżyc porusza się po orbicie w przybliżeniu eliptycznej. Dokładna orbita eliptyczna występuje w zagadnieniu dwóch ciał. Księżyc obiega Ziemi, ponadto doznaje oddziaływania grawitacyjnego ze strony Słońca, ciała, które najbardziej zaburza jego ruch. Ponadto na ruch Księżyca wpływa, w mniejszym stopniu Wenus oraz Jowisz. W efekcie ruch obiegowy Księżyca odbywa się po orbicie w przybliżeniu eliptycznej. Z II prawa Keplera wiadomo, że prędkość liniowa z jaką porusza się Księżyc po orbicie nie jest stała, podobnie jak jego prędkość kątowa w ruchu orbitalnym. Kiedy Księżyc znajduje się w perygeum swojej orbity wówczas porusza się z największą prędkością zatem jego prędkość kątowa ruchu orbitalnego jest większa od prędkości kątowej jego rotacji wokół własnej osi. W apogeum mamy sytuację odwrotną, prędkość kątowa ruchu orbitalnego jest mniejsza od jego prędkości kątowej rotacji wokół własnej osi. Zatem czy wybrany przez obserwatora punkt będzie zachowywał stałe położenie względem obserwatora? Szybka analiza wskazuje, że nie. Rozważania rozpocznijmy od sytuacji, kiedy Księżyc znajduje się w średniej odległości od Ziemi, przy której prędkość kątowa w ruchu obiegowym jest równa prędkości kątowej rotacji Księżyca wokół własnej osi. Kiedy Księżyc kontynuuje swój ruch orbitalny zwiększając swoją odległość, prędkość kątowa w ruchu orbitalnym staje się mniejsza od prędkości kątowej jego rotacji. Skutkuje to tym, że punkt zaczyna się pozornie przesuwać na wschód. Oczywiście dotyczy to wszystkich jego punktów powierzchni. Kiedy punkty przesuwają się względem obserwatora na wschód obserwatorowi ukazują się także obszary zalegające za wschodnią krawędzią. Oznacza to, że obserwatorowi zaczyna ukazywać się fragment powierzchni za wschodniej krawędzi. Początkowo fragment ma niewielkie rozmiary, jednak w miarę upływu czasu, jak Księżyc zaczyna zbliżać się do apogeum orbity człowiek może obserwować coraz większy obszar za wschodniej jego krawędzi. Księżyc znajdujący się w apogeum porusza się najwolniej, a więc zostaje odsłonięty maksymalnie wschodni fragment. Po minięciu apogeum Księżyc zaczyna zbliżać się do Ziemi, zwiększa swoją prędkość kątową, dostępny do obserwacji fragment powierzchni za wschodniej krawędzi zmniejsza się, a wybrany przez nas punkt porusza się w kierunku zachodnim. Kiedy Księżyc osiągnie pozycję na orbicie, w której następuje zrównanie prędkości kątowej ruchu orbitalnego i rotacyjnego, wybrany punkt osiągnie stan początkowy, z którego rozpoczęliśmy analizę. Księżyc kontynuując ruch zaczyna się poruszać z prędkością kątową większa od prędkości kątowej rotacji wokół własnej osi. Wybrany punkt w dalszym ciągu porusza się w kierunku zachodnim, a obserwator ma możliwość obserwacji zachodniego fragmentu wyłaniającego się z zachodniej krawędzi powierzchni, które wcześniej była niedostępna obserwacjom. W perygeum Księżyc porusza się z największą prędkość, wybrany punkt przesunął się maksymalnie na zachód, a obserwator może podziwiać największy fragment powierzchni, który wyłoniła się z zachodniej jego krawędzi. Przy dalszym ruchu prędkość liniowa jak kątowa w ruchu orbitalnym maleje, Księżyc oddala się od Ziemi, wybrany punkt zaczyna poruszać się w kierunku wschodnim, zachodni obszar za zachodniej krawędzi dostępny obserwacją maleje. Wybrany punkt osiąga wyjściowe położenie, kiedy następuje zrównanie prędkości kątowych ruchu orbitalnego i rotacji wówczas obserwator nie ma możliwości podziwiania elementów powierzchni za zachodniej krawędzi jego powierzchni. Śledząc ruch wybranego punktu na powierzchni Księżyca obserwator z Ziemi odnosi wrażenie jakby wybrany punkt, a tym cała bryła księżycowa, wykonywał (wykonywała) ruch drgający wschód-zachód. Tego typu zjawisko nazywa się libracją w długości. W wyniku tego zjawiska człowiek ma możliwość zaobserwowania obszarów Księżyca o długości selenograficznej ±97°54’ [7,8]. Okres libracji w długości wynosi dokładnie tyle i trwa miesiąc anomalistyczny, czyli czas jaki upływa między dwoma przejściami Księżyca przez perygeum orbity i jest nieznacznie dłuższy od okresu gwiazdowego. Średnia długość miesiąca anomalistycznego wynosi 27^d13^h18^m33^s [9]. W wyniku perturbacji orbity długość miesiąca nie jest stała. Głównym źródłem zaburzeń jest Słońce. Kiedy różnica w długości ekliptycznej Słońca i perygeum wynosi 0° lub 180° wówczas długość miesiąca anomalistycznego jest najdłuższa i wynosi 28,5 dnia [9]. Przy różnicy w długości wynoszącej 90° lub 270° miesiąc anomalistyczny jest krótszy od średniego miesiąca anomalistycznego. Ponieważ Słońce powoduje perturbacje w związku z tym odległość Ziemi od Słońca również będzie wpływać na okres jaki upływa między dwoma przejściami Księżyca przez perygeum orbity. Kiedy różnica w długości ekliptycznej perygeum Księżyca i peryhelium Ziemi wynosi 0° wówczas długość miesiąca anomalistycznego jest ekstremalnie długa i wynosi 28 dni 13 godzin [10]. Najkrótszy miesiąc anomalistyczny wynosi 24 dni i 16 godzin [10]. Jako ciekawostkę, można rozpatrzeć interwał czasu między dwoma przejściami Księżyca przez apogeum orbity. Okazuje się, że zmienność różnicy interwałów czasu (różnica czasu między aktualną i średnią długością miesiąca anomalistycznego) między dwoma przejściami Księżyca przez apogeum jest mniejsza w porównaniu z różnicą interwałów czasowych przejścia Księżyca przez perygeum i waha się od 26 dni i 23,5 godzin do 27 dni i 21,5 godzin [10].

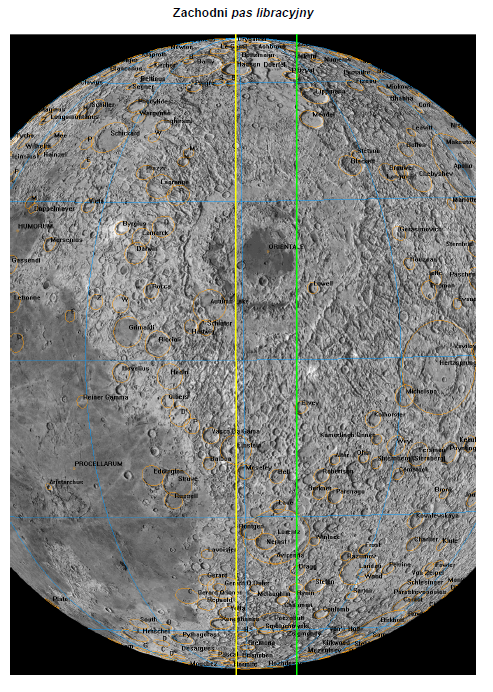
Ryc. 1. Zachodni i wschodni pas libracyjny. Źródło: Tomasz Ściężor, Almanach Astronomiczny na rok 2024, PTA, Warszawa, 2023.

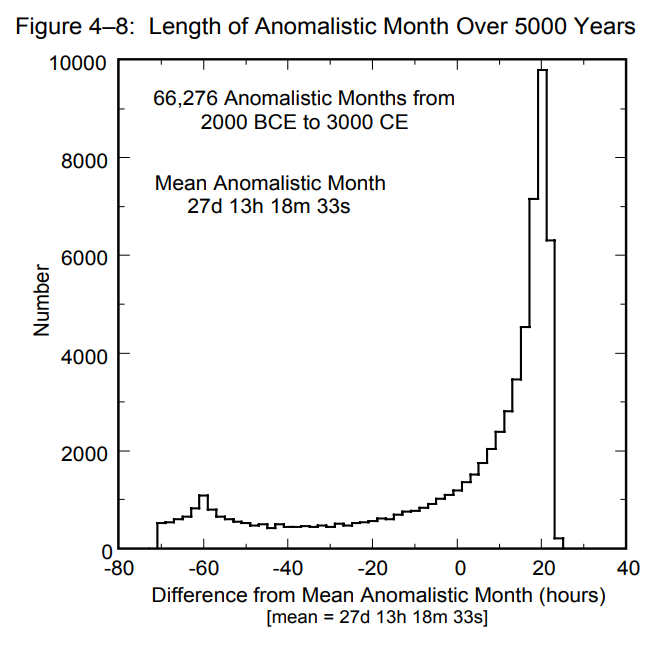
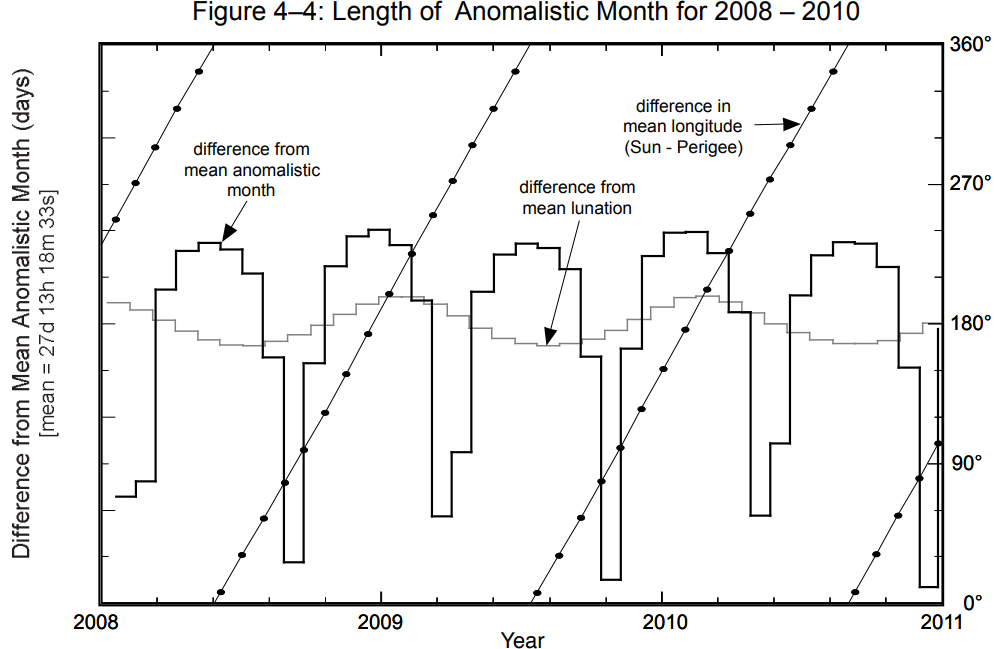
Ryc. 2. Długość miesiąca anomalistycznego na przestrzeni 5000 lat (histogram – lewy) i w okresie 2008-2010 (prawy). Źródło: Fred Espenak and Jean Meeus, Five Millennium Catalog of Solar Eclipses: -1999 to +3000 (2000 BCE to 3000 CE)-Revised, NASA/TP – 2009-214174.

Szerokość zachodniego lub wschodniego pasa libracyjnego zależeć będzie od mimośrodu orbity księżycowej. Wiadomo, że Księżyc porusza się po orbicie o średnim mimośrodzie 0,0549. Jednak w wyniku perturbacji jego orbity wartość mimośrodu się zmienia. Z analizy obejmującej 5000 lat przeprowadzonej przez Jeana Meeusa wynika, że wartość mimośrodu zmienia się w granicach 0,0255 do 0,0775 [6,9]. Ekscentryczność orbity księżycowej osiąga maksimum, kiedy oś węzłów pokrywa się z kierunkiem Słońca, czyli kiedy długość ekliptyczna Słońca i perygeum jest taka sama lub wynosi 180°. Minimum mimośrodu orbity jest osiągany wtedy, kiedy oś węzłów jest prostopadła do kierunku Słońca (różnica w długości ekliptycznej Słońca i perygeum wynosi 90° lub 270°).

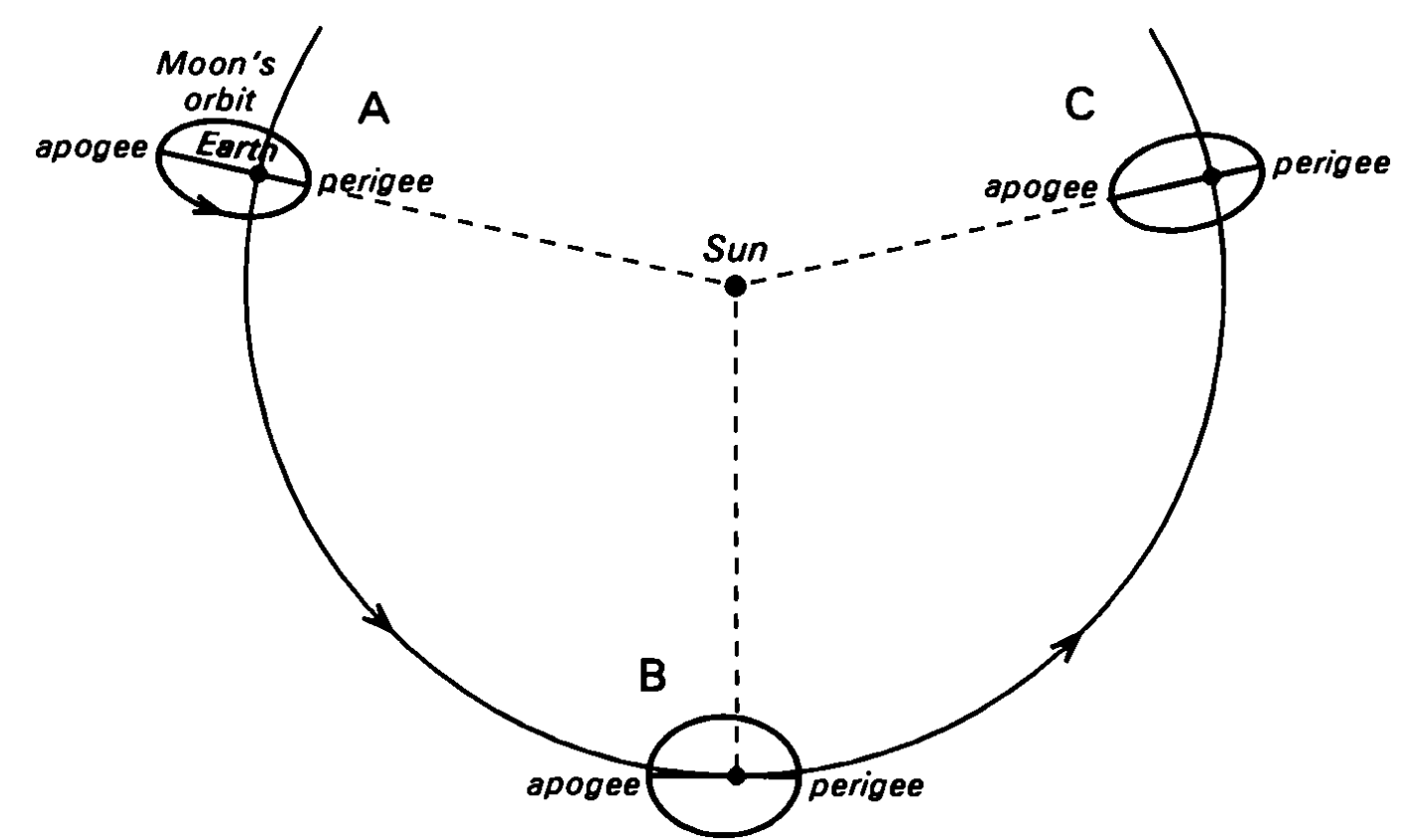
Ryc. 3. Maksimum mimośrodu orbity występuje wtedy, kiedy oś węzłów pokrywa się z kierunkiem do Słońca (A) oraz (C). Minimum mimośrodu orbity księżycowej występuje wtedy, kiedy oś węzłów jest prostopadła do kierunku Słońca (B). Źródło: Jean Meeus, Mathematical Astronomy Morsels, Willman-Bell, Inc, 1997.

Czas jaki upływa między maksimum i minimum mimośrodu wynosi 103 dni, natomiast między dwoma maksimami mimośrodu wynosi 205,9 dni [9]. Wraz ze wzrostem mimośrodu prędkość liniowa jak i kątowa zwiększa osiągając maksimum w perygeum zatem ze wzrostem wielkości mimośrodu wzrasta szerokość libracyjnego pasa wschodniego i zachodniego. Przy zmniejszaniu mimośrodu zmniejsza się szerokość pasa libracyjnego zarówno zachodniego i wschodniego.

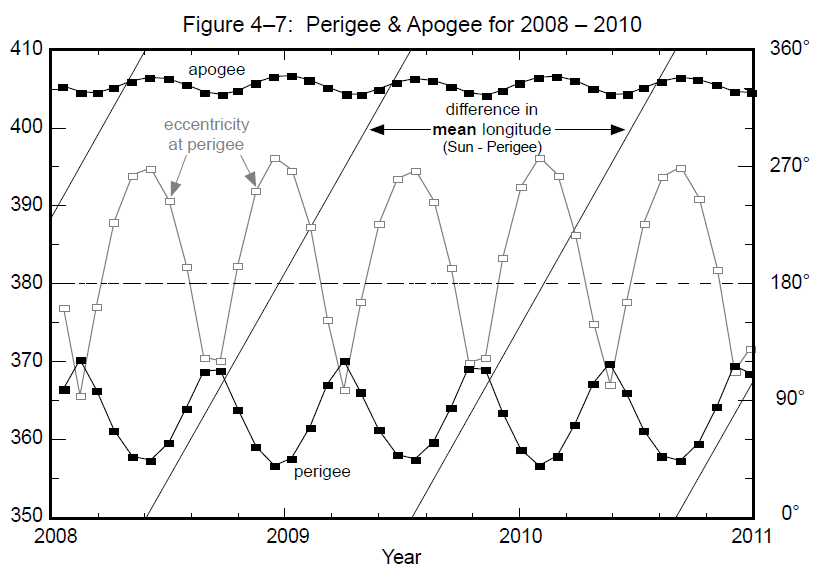
Ryc. 4. Odległość Księżyca w perygeum i apogeum orbity w funkcji różnicy w długości ekliptycznej Słońca i perygeum. Źródło: Fred Espenak and Jean Meeus, Five Millennium Catalog of Solar Eclipses: -1999 to +3000 (2000 BCE to 3000 CE)-Revised, NASA/TP – 2009-214174.

Libracje w szerokości

   Drugie prawo Cassiniego tłumaczy libracje w szerokości. Z prawa tego dowiadujemy się, że oś obrotu Księżyca jest nachylona do płaszczyzny jego orbity pod kątem 83°18’ [8] i zachowuje stałe położenie w przestrzeni. Podczas ruchu orbitalnego Księżyca raz biegun północny Księżyca nachylony jest w kierunku Ziemi co umożliwia obserwować obszary znajdujące się poza biegun północnym. Innym razem biegun południowy Księżyca nachylony jest w kierunku Ziemi i można podziwiać obszary znajdujące się za biegunem południowym. Maksymalnie możemy obserwować obszary za biegunem do szerokości selenograficznej 83°18’. To czy biegun południowy czy północny skierowany jest w kierunku Ziemi zależy od położenia Księżyca na orbicie. Kiedy Księżyc porusza się po fragmencie orbity zawartej między węzłem wstępującym i zstępującym (co trwa połowę miesiąca smoczego), czyli kiedy orbita księżycowa przecina północne rejony sfery niebieskiej wówczas w kierunku Ziemi skierowany jest biegun południowy Księżyca. Natomiast kiedy Księżyc porusza się po fragmencie orbity między węzłem zstępującym i wstępującym, czyli wtedy, kiedy orbita księżyca przecina południowy obszar sfery niebieskiej (druga połowa miesiąca smoczego) wówczas w kierunku Ziemi skierowany jest biegun północny Księżyca. Analizując ruch wybranego punktu na powierzchni Księżyca względem ziemskiego obserwatora człowiek odnosi wrażanie jakby wybrany punkt (ale także cała bryła Srebrnego Globu) wykonywał ruch drgający w kierunku północ-południe. Okres libracji w długości równa się miesiącowi smoczemu, czyli okresowi jako upływa między dwoma przejściami Księżyca przez węzeł swojej orbity, który jest krótszy od miesiąca gwiazdowego, a to dlatego, że ruch węzłów odbywa się w kierunku przeciwnym (ruchem retrogradacyjnym) do kierunku ruchu Księżyca. Librację w szerokości została odkryta w 1637 roku przez Galileusza. Średnia długość miesiąca smoczego wynosi 27^h05^m05^m36^s [9]. W wyniku perturbacji orbity księżycowej długość miesiąca smoczego zmienia się. Najdłuższe miesiące smocze występują, kiedy średnia długość ekliptyczna Słońca i węzła wstępującego wynosi 0° lub 180°. Najkrótszy, kiedy różnica w średniej długości ekliptycznej Słońca i węzła wstępującego wynosi 90° i 270°. Okres zmian w długości miesiąca smoczego wywołanych powyższymi czynnikami wynosi 173,3 dnia. Na długość miesiąca smoczego wpływa także położenie perygeum orbity księżycowej względem węzła wstępującego. Największe ekstrema w długości miesiąca smoczego występują wtedy, kiedy kąt między perygeum i węzłem wynosi zero, czyli wtedy, kiedy linia apsyd pokrywa się z osią węzłów. Najmniejsze ekstrema w miesiącu smoczym występują wtedy, kiedy oś węzłów i linia apsyd są wzajemnie prostopadłe [9]. Okres zmian w długości miesiąca smoczego wywołany powyższym efektem wynosi 2190,35 dnia. Na długość miesiąca smoczego wpłynie także nałożenie się obu efektów, czyli wtedy kiedy długość ekliptyczna Słońca, węzła wstępującego oraz perygeum jest taka sama.

Ryc. 5. Północny i południowy pas libracyjny. Źródło: Tomasz Ściężor, Almanach Astronomiczny na rok 2024, PTA, Warszawa, 2023.

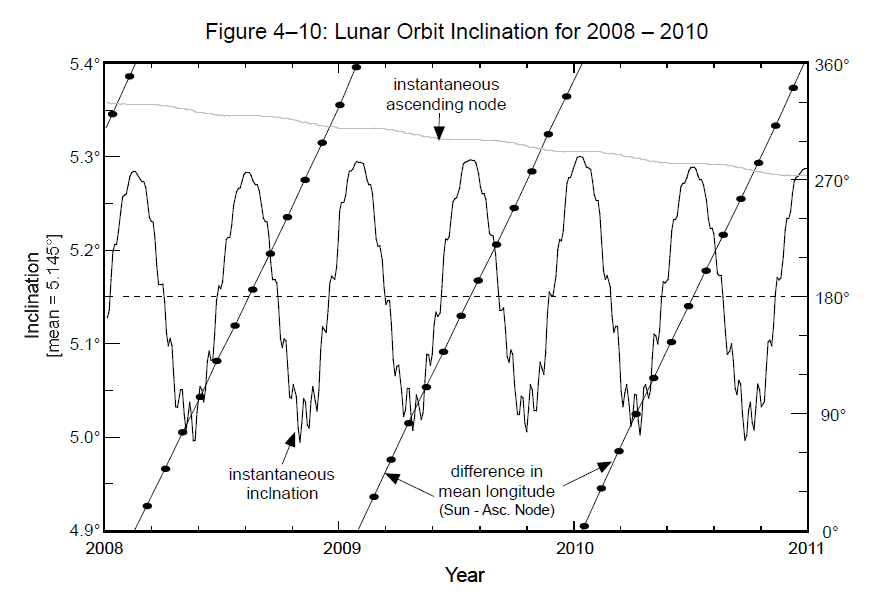
Ryc. 6. Długość miesiąca smoczego w zależności od różnicy średniej długości ekliptycznej Słońca i węzła wstępującego. Źródło: Źródło: Fred Espenak and Jean Meeus, Five Millennium Catalog of Solar Eclipses: -1999 to +3000 (2000 BCE to 3000 CE)-Revised, NASA/TP – 2009-214174.

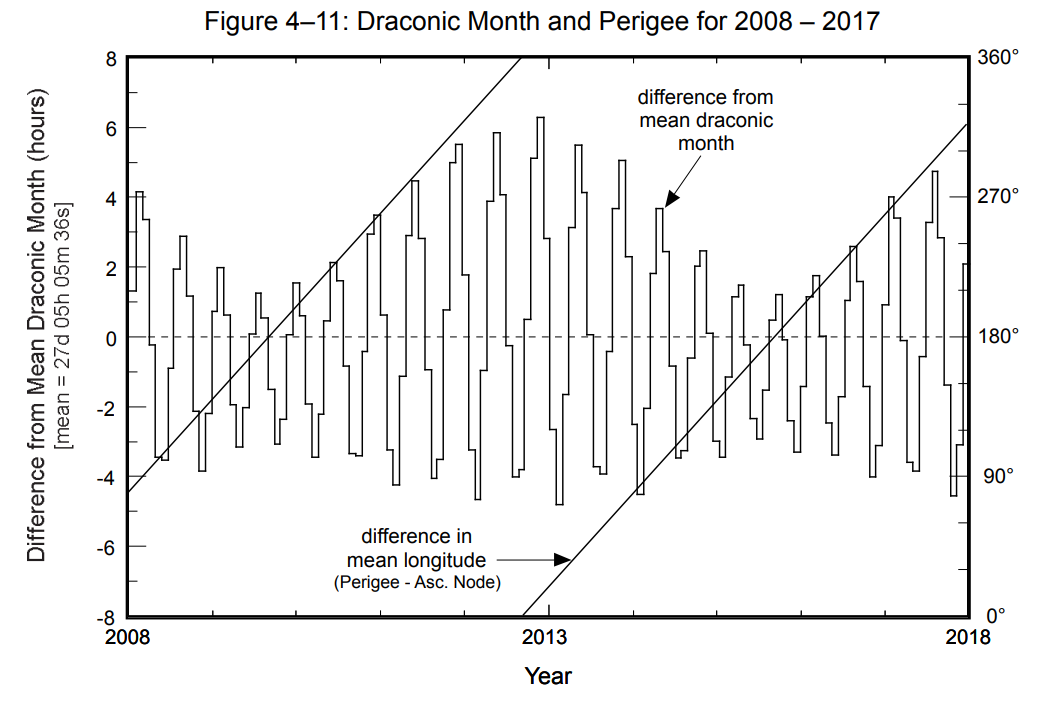
Ryc. 7. Długość miesiąca smoczego w zależności od różnicy średniej długości ekliptycznej perygeum i węzła wstępującego. Źródło: Źródło: Fred Espenak and Jean Meeus, Five Millennium Catalog of Solar Eclipses: -1999 to +3000 (2000 BCE to 3000 CE)-Revised, NASA/TP – 2009-214174.

Z analizy okresu obejmującego 5000 lat wynika, że najkrótszy miesiąc smoczy wynosi 27 dni 5 minut i 45,6 sekund, natomiast najdłuższy miesiąc smoczy wynosi 27 dni 11 godzin 41 minut 16,8 sekund [9]. Ponieważ linia apsyd porusza się w przestrzeni ruchem dyrekcyjnym, a oś węzłów ruchem retrogradacyjnym to średni czas jaki upływa między dwoma położeniami, kiedy perygeum pokrywa się z węzłem wstępującym wynosi 2190,35 dnia [9]. Szerokość północnego i południowego pasa libracyjnego zależy także różnicy w długości ekliptycznej węzła wstępującego i punktu równonocy wiosennej (punkt Barana). Kiedy węzeł wstępujący znajduje się w punkcie Barana wówczas szerokość północnego i południowego pasa libracyjnego będzie największa. Kiedy różnica w długości ekliptycznej węzła wstępującego i punktu Barana wyniesie 180° wówczas szerokość północnego i południowego pasa libracyjnego osiąga najmniejsze rozmiary.

Libracje dzienne (paralaktyczne)

   Trzecim rodzajem libracji jest libracja dzienna lub inaczej paralaktyczna. Ten rodzaj libracji jest zależy od położenia Księżyca nad horyzontem, a to jest związane z ruchem obrotowym Ziemi wokół własnej osi oraz od położenia obserwatora na powierzchni Ziemi. Obserwując wybrany punkt na powierzchni Księżyca z dwóch różnych położeń na Ziemi lub przy dwóch różnych położeniach Księżyca na sferze niebieskim w danym punkcie na powierzchni Ziemi zauważyć można, że położenie np. wybranego punktu na powierzchni Księżyca względem obserwatora ziemskiego zmieni się. Wielkość libracji dziennych równe są paralaksie geocentrycznej, która maksymalnie może osiągać wartość 1°01,5’ [11]. Kiedy Księżyc wschodzi obserwator znajdujący się na powierzchni Ziemi będzie widział obszar znajdujący się za zachodnim brzegu tarczy Księżyca w porównaniu z obserwatorem, który by został umieszczony w centrum Ziemi. Kiedy Księżyc zachodzi wówczas obserwator z powierzchni Ziemi będzie miał możliwość zajrzeć za wschodni brzeg tarczy Księżycowej [7]. Okres libracji paralaktycznych równa się obrotowi Ziemi wokół własnej osi.

Libracje fizyczne

   Powyższe trzy rodzaje libracje znajdują wytłumaczenie na gruncie trzech empirycznych praw Cassiniego. Jednak, kiedy się im dokładnie przyjrzymy to okazuje się, że nie są one ściśle spełnione. Libracje fizyczne są skutkiem odstępstw od ww. praw. W pierwszym prawie Cassiniego stwierdza się, że ruch obrotowy Księżyca wokół własnej osi jest stały co nie jest do końca prawdą. Odstępstwo od I prawa Cassiniego skutkuje libracjami fizycznymi wymuszonymi w długości [5]. Obecnie wiadomo, że nachylenie płaszczyzny równika Księżyca względem płaszczyzny ekliptyki również nie stałe i waha się w granicach ±24” [11], co skutkuje fizycznymi libracjami wymuszonymi w nachyleniu i jest to efekt odstępstwa od II prawa Cassiniego [5]. Położenie węzłów orbity i płaszczyzny równika księżycowego również nie zachowują stałego położenia względem siebie co prowadzi do fizycznych libracji wymuszonych w węźle i jest to efekt odstępstwa od III praca Cassiniego [5]. Dodatkowo należy uwzględnić niestałość położenia osi obrotu Księżyca w jego wnętrzu co prowadzi do fizycznych libracji dowolnych (swobodna nutacja osi księżycowej), które odpowiadają perturbacji Eulera. Maksymalne libracje fizyczne wynoszą do 2’ długości selenograficznej i do 3’ szerokości selenograficznej [6].

W wyniku tych czterech rodzajów libracji obserwator ziemski może obserwować 59% powierzchni.

Całość komponuje się w dość skomplikowany obraz ruchu Księżyca i widoczność jego powierzchni z Ziemi, opisany jako chybotanie, chwianie się (ang. wobbling). Można go podejrzeć na stronie APOD (Astronomical Picture Of the Day) z 1999 r.: https://apod.nasa.gov/apod/ap991108.html

Z całej tej opowieści warto pamiętać, że libracja powyżej 10 stopni (złożenie libracji w długości i w szerokości) oznacza, że brzeg zazwyczaj niewidocznej dla nas części tarczy księżycowej jednak ku nam się zwraca. Katalogi zazwyczaj podają właśnie librację w długości i librację w szerokości jako miary odchylenia początku współrzędnych księżycowych (takiego księżycowego Greenwich) od kierunku wprost na Ziemię.

I takie właśnie wydarzenie ma zajść 4 marca 2024 roku. Czwartego marca 2024 roku o godzinie 22 libracje osiągną wartość 10°12’. Wówczas maksymalnie oświetlony będzie sektor Sinus Iridium [12].

Ryc. 8. Obszar libracyjny, który w danym momencie „wyłoni się” na brzegu tarczy Księżyca. Źródło: Tomasz Ściężor, Almanach Astronomiczny na rok 2024, PTA, Warszawa, 2023.

Krzywe kreślone przez punkty na powierzchni Księżyca w wyniku libracji

   Powyżej przedstawiono mechanizm libracji optycznych oraz fizycznych. W ruchu orbitalnym Księżyc doznaje libracji zarówno w długości, szerokości, paralaktycznej oraz fizycznych. Zatem punktu na powierzchni Księżyca obserwowane przez człowieka z Ziemi będzie zakreślał ciekawe krzywe, które powstają w wyniku złożenia wszystkich libracji. Libracje fizyczne oraz paralaktyczną pomińmy w naszych rozważaniach a to dlatego, że ich wpływ na kształt trajektorii punktu względem obserwatora będzie nieznaczny. Rozważmy punkt znajdujący się na środku tarczy księżycowej, czyli punkt o współrzędnych 0° szerokości i długości selenograficznej.

Rozważmy sytuację, kiedy Księżyc znajduje się w perygeum orbity oraz przechodzi przez węzeł wstępujący orbity, czyli długość ekliptyczna perygeum i węzła wstępującego jest taka sama. Kiedy Księżyc oddala się od perygeum orbity oraz od węzła wstępującego wówczas punkt na powierzchni Księżyca będzie poruszał się względem obserwatora na Ziemi po krzywej będącą złożeniem ruchu punktu w kierunku wschodnim (libracja w długości) i w kierunku północnym (libracja w szerokości). Kiedy Księżyc będzie oddalał się od apogeum oraz od węzła zstępującego wówczas punkt na powierzchni Księżyca będzie poruszał się w kierunku zachodnim (libracja w długości) i w kierunku południowym (libracja w szerokości). Złożenie tych dwóch libracji spowoduje, że punkt obserwowany z Ziemi będzie pozornie poruszał się po linii prostej (jak w przykładzie na ryc. 1. October 1994) [6]. Podobny kształt pozornej trajektorii będzie można obserwować, kiedy długości ekliptyczne perygeum i długość węzła wstępującego będą się różnić o 180°. Jest to sytuacja, kiedy Księżyc jest w perygeum orbity i w węźle zstępującym. Kiedy Księżyc oddala się od Ziemi (od perygeum) poruszając się po południowej sferze niebieskiej, czyli od węzła zstępującego do wstępującego, wówczas punkt pozornie będzie poruszał się w kierunku wschodnim (libracja w długości) i na południe (libracja w szerokości). Złożenie tych dwóch pozornych ponownie spowoduje, że pozorna trajektoria będzie linią prostą, ale innej orientacji (jak w przykładzie na ryc. 1. September 1997) [6]. Kiedy różnica w długości ekliptycznej perygeum i węzła wstępującego zwiększa się od zera wówczas pozorna trajektoria zaczyna przypominać zdeformowaną niezamkniętą lub zamkniętą krzywą, której mała „półoś” zwiększa się wraz ze zwiększaniem się różnicy w długości ekliptycznej perygeum oraz węzła wstępującego. Zakreślana pętla osiąga maksymalne rozmiary wtedy, kiedy oś linii apsyd i linii węzłów jest prostopadła względem siebie (jak w przykładzie na ryc. 1. March 1996) [6]. Przy dalszym zwiększaniu różnicy w długości ekliptycznej perygeum i węzła wstępującego mała „półoś” zakreślanej krzywej zacznie maleć, zdeformowany owal będzie coraz węższy. Kiedy perygeum orbity pokrywa się z węzłem zstępującym co oznacza, że kiedy Księżyc znajduje się w perygeum orbity jest równocześnie w węźle zstępującym swojej orbity wówczas pozorna trajektoria jest linią prostą (jak w przykładzie na ryc. 1. September 1997) [6]. Kiedy różnica w długości ekliptyczna perygeum i węzła zstępującego się zwiększa, pozorną trajektorią jest linią krzywą przypominającą zdeformowaną niedomknięty owal o zwiększających się rozmiarach. Krzywa osiąga maksymalne rozmiary, kiedy ponownie oś linii węzłów i apsyd są prostopadłe względem siebie. Kiedy różnica w długości ekliptycznej perygeum i węzła wstępującego ponownie osiągnie zero stopni, wówczas powracany do stanu wyjściowego, gdzie pozorną trajektorią punktu na Księżycu względem obserwatora na Ziemi jest linia prosta. Zdeformowane owale wynikają z faktu dość złożonego ruchu orbitalnego Księżyca.

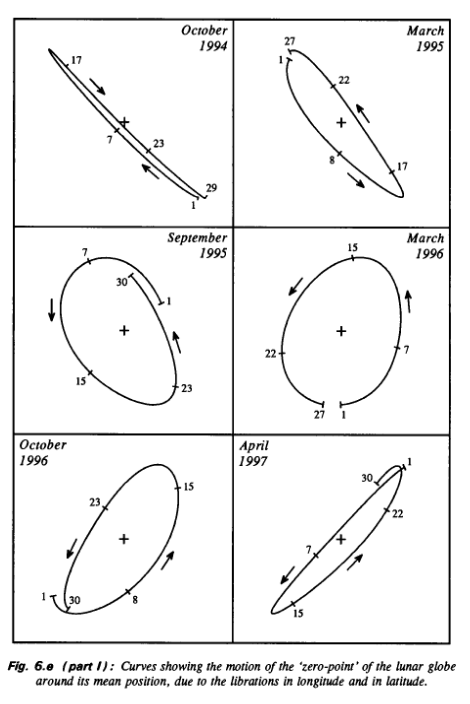
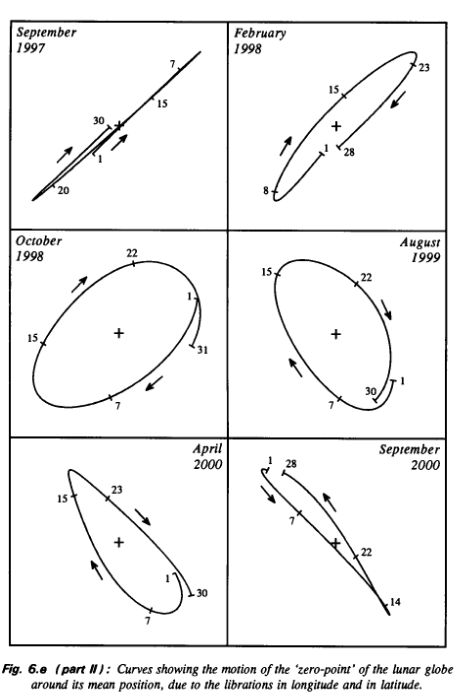
Ryc. 9. Krzywe kreślone przez wybrany punkt na powierzchni Księżyca względem obserwatora w wyniku złożenia libracji w długości i szerokości. Źródło: Jean Meeus, Mathematical Astronomy Morsels, Willman-Bell, Inc, 1997.

Linia apsyd porusza się ruchem dyrekcyjnych przesuwając się o 0,11140° na wschód zaś węzły ruchem retrogradacyjnym z szybkością 0,05295° na zachód [6,9].

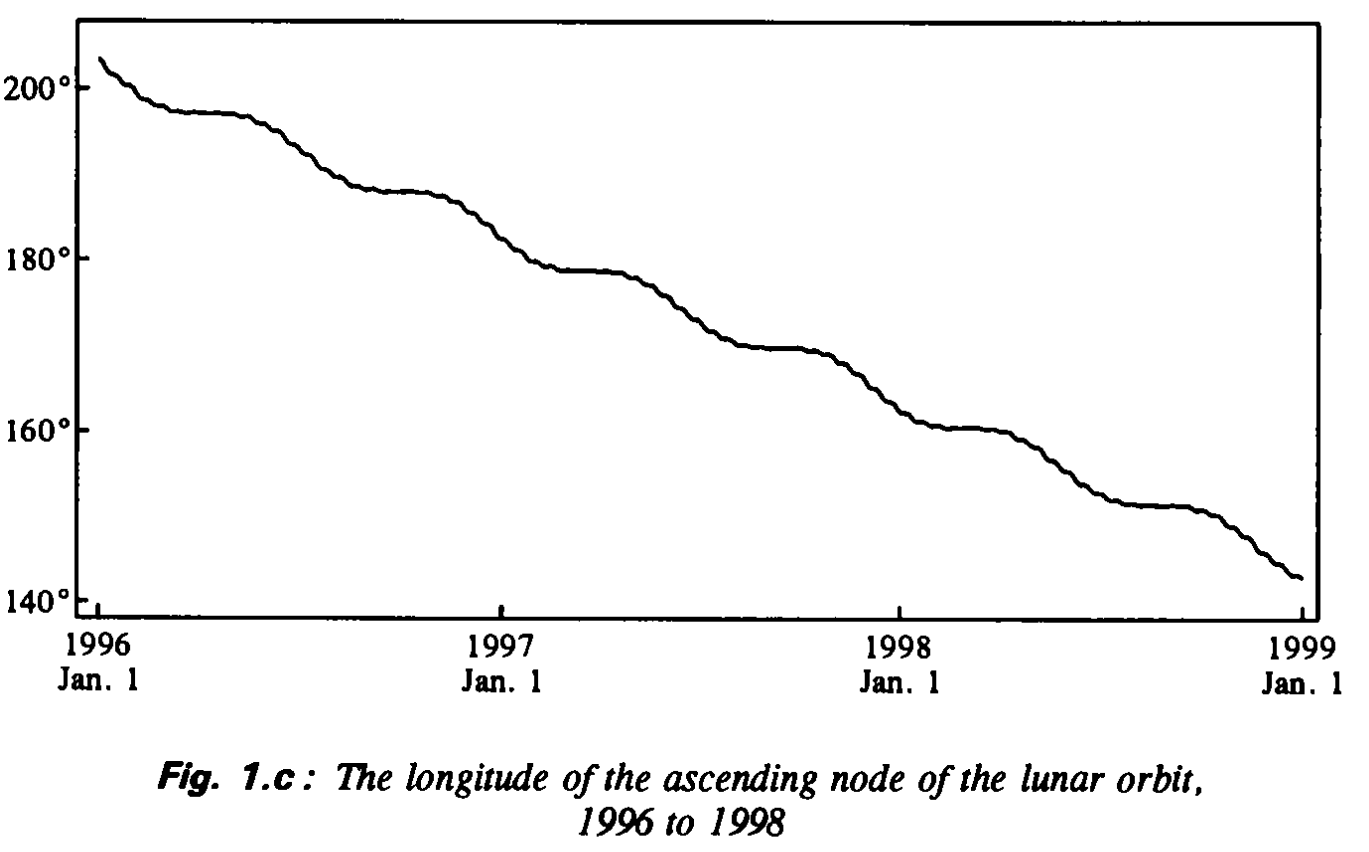
Ryc. 10. Zmiana w czasie długości ekliptycznej węzła wstępującego Księżyca w latach 1996-1998. Źródło: Jean Meeus, Mathematical Astronomy Morsels, Willman-Bell, Inc, 1997.

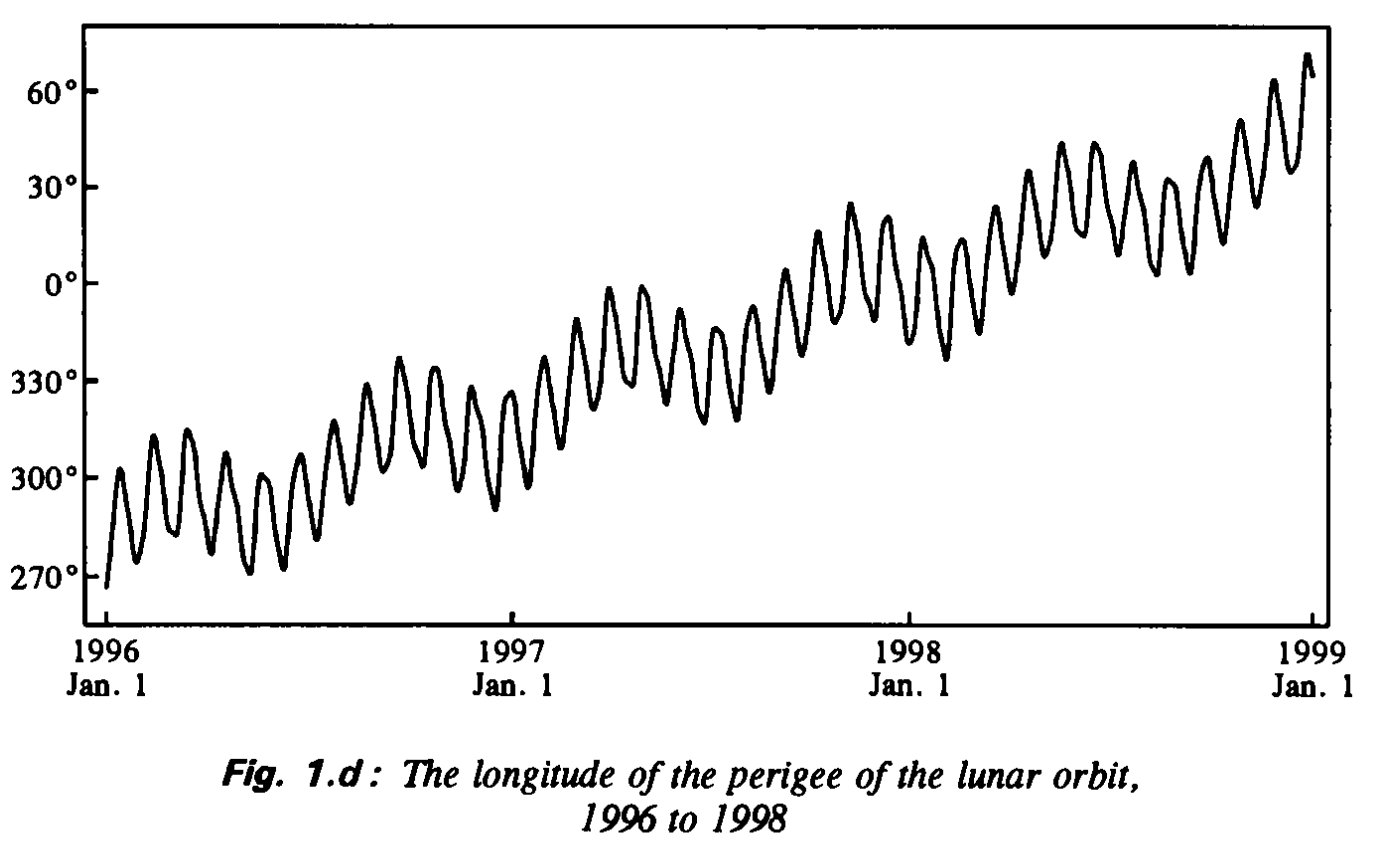
Ryc. 11. Zmiana w czasie długości ekliptycznej perygeum orbity Księżyca w latach 1996-1998. Źródło: Jean Meeus, Mathematical Astronomy Morsels, Willman-Bell, Inc, 1997.

Proste obliczenia wskazują, że czas jaki upływa między dwoma kolejnymi położeniami perygeum i węzła wstępującego, kiedy ich różnica w długości wynosi zero stopni, czyli wtedy, kiedy linia apsyd i osi węzłów pokrywa się wynosi 2190,35 dni. Zatem pełen cykl złożonych libracji w długości i szerokości wynosi prawie 6 lat [9].

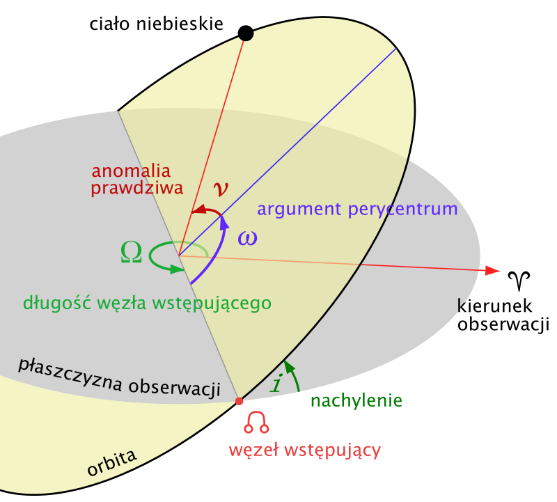
Ryc. 12. Elementy orbity przykładowego ciała niebieskiego – w naszym przypadku, Księżyca wokół Ziemi. Źródło: Wikipedia.

Rozmaitości

   Sama ludowa nazwa Księżyca – „miesiąc” – odnosi się do faktu, że fazy Księżyca wyznaczały rytm miesięczny a obieg Ziemi wokół Słońca – roczny. Takich ‘miesięcy” jest kilka: gwiazdowy (syderyczny), smoczy, synodyczny, anomalistyczny czy tropikalny – w zależności, jakie zjawisko opisujemy (czy np. ruch węzłów orbity księżycowej, ruch na tle gwiazd, kiedy Księżyc przechodzi przez kolejne perygea, czy kiedy Księżyc przechodzi przez ten sam południk niebieski).

Ryc. 13. Karta tytułowa I wydania powieści „Faraon” B. Prusa (pseudonim literacki Aleksandra Głowackiego). Źródło: Wikipedia.

Nieco podobnym do różnych rodzajów miesięcy jest zjawisko cyklu saros zaćmień Słońca. Był on istotny ze względu na możliwość ich przepowiedzenia (co nie było wiedzą powszechną) i tym samym, sterowania nastrojami dużych grup ludzkich – wystarczy przywołać scenę z „Faraona” Bolesława Prusa.

Literatura:

1. P. Artymowicz, Astrofizyka układów planetarnych, PWN, 1995.
2. W. W. Bielecki, Szkicde o ruchach ciał niebieskich, PWN, 1976.
3. J. Chambers, J. Mittion, Od pyłu do życia – Pochodzenie i ewolucja Układu Słonecznego, PWN, 2018.
4. Sz. Szczeniowski, Fizyka doświadczalna – część I, PWN, 1980.
5. J. Mietelski, Astronomia w geografii, PWN, 2001.
6. J. Meeus, Mathematical Astronomy Morsels, Willman-Bell, Inc, 1997.
7. E. Rybka, Astronomia ogólna, PWN, wyd. VII, 1983.
8. J. Kreiner, Ziemi i Wszechświat – astronomia nie tylko dla geografów, Wydawnictwo Naukowe Uniwersytetu Pedagogicznego, Kraków, 2009.
9. F. Espenak and J. Meeus, Five Millennium Catalog of Solar Eclipses: -1999 to +3000 (2000 BCE to 3000 CE)-Revised, NASA/TP – 2009-214174.
10. J. Meeus, Astronomical Algorithms, 2^nd Willman-Bell, Inc, 1998.
11. Z. Dworak, Z astronomią za pan brat, Wydawnictwo Iskry, Warszawa, 1989.
12. T. Ściężor, Almanach Astronomiczny na rok 2024, PTA, Warszawa, 2023.
13. Astronomical Picture of the Day, 8.11.1999.
14. Wikimedia Commons.
15. astropical.space.
16. strona: https://svs.gsfc.nasa.gov/5187/ z animacją libracji Księżyca.

 

 

— UDOSTĘPNIJ —