Zjawisko halo
28.11.2022
Opracował: dr Grzegorz Duniec, CMM IMGW-PIB
Zjawisko optyczne halo należy do grupy fotometeorów. Zgodnie z definicją fotometeor to zjawisko świetlne powstające wskutek odbicia, załamania, ugięcia lub interferencji światła słonecznego lub księżycowego [1,2].
Halo to grupa zjawisk optycznych w postaci pierścieni, łuków, słupów lub plam świetnych, powstających wskutek załamania lub odbicia światła przez kryształki lodu unoszące się w powietrzu (chmury piętra wysokiego, pył diamentowy, mgła lodowa) [1,2].
Zjawisko halo wytworzone przez światło słoneczne stanowi kolorowe pierścienie, natomiast wytworzone przez światło księżycowe tworzy białe okręgi.
W wyniku załamania promieni słonecznych w kryształkach lodu można obserwować zjawiska optyczne należących do grupy zjawisk typu halo:
a) mały pierścień halo – tzw. 22° halo;

Źródło: https://cloudatlas.wmo.int/en/search-image-gallery.html
b) duży pierścień halo – tzw. 46° halo;

Źródło: https://cloudatlas.wmo.int/en/search-image-gallery.html
c) słup świetlny;

Źródło: https://cloudatlas.wmo.int/en/search-image-gallery.html
d) łuk styczny górny;

Źródło: https://cloudatlas.wmo.int/en/search-image-gallery.html
e) łuk styczny dolny;
f) łuk Parry’ego;
g) łuk Lowitza;
h) łuk okołozenitalny górny;

Źródło: https://cloudatlas.wmo.int/en/search-image-gallery.html
i) łuk okołozenitalny dolny;
j) łuk okołohoryzontalny;

Źródło: https://cloudatlas.wmo.int/en/search-image-gallery.html
k) łuk poboczny dolny;
l) poziomy krąg przysłoneczny;
m) Słońce dolne (pozorne) zwane też Słońcem pobocznym.

Źródło: https://cloudatlas.wmo.int/en/search-image-gallery.html
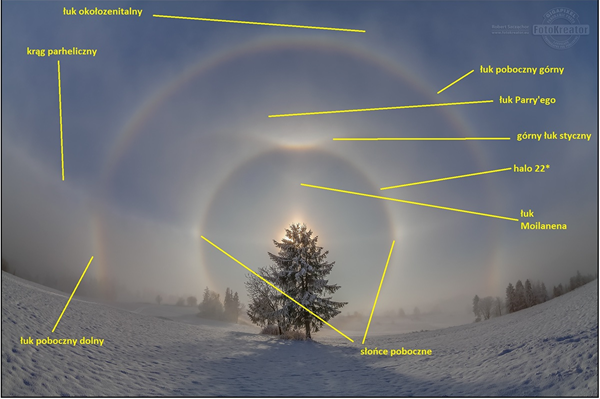
Źródło: https://www.behance.net/gallery/34258251/Zjawiska-optyczne
Spojrzymy teraz na zjawiska optyczne z punktu widzenia fizyki. Rozpoczniemy od omówienia halo w postaci małego lub dużego pierścienia wokół Słońca lub Księżyca.
Międzynarodowa Organizacja Meteorologiczna definiuje mały oraz duży pierścień halo w następujący sposób [1,2]:
Mały pierścień halo – jest to krąg świetlny, barwny, biały lub w przeważającej części biały, o promieniu 22°, w którego środku znajduje się tarcza Słońca lub Księżyca. Krąg ten ma zwykle słabo widoczne zabarwienie czerwone od wewnątrz i w rzadkich przypadkach fioletowe zabarwienie na zewnątrz. Część nieba wewnątrz kręgu jest wyraźnie ciemniejsza niż na zewnątrz.
Duży pierścień halo – jest to krąg świetlny o promieniu 46°; jest on zawsze mniej jasny i o wiele rzadziej obserwowany niż mały pierścień halo.
Chmury mieszane lub chmury lodowe zbudowane są z kryształków lodowych. W chmurach mieszanych dodatkowo znaleźć można kropelki wody, których część będzie przechłodzona (w obszarze chmury znajdującej się powyżej izotermy zero). Kryształki lodu przyjmują różne kształty.

Źródło: H. R. Pruppacher, J. D. Klett, Microphysics of Clouds and Precipitation , Second edition, Springer Dordrecht, 2010.
W oparciu o obserwacje stworzono klasyfikację kryształków lodu.
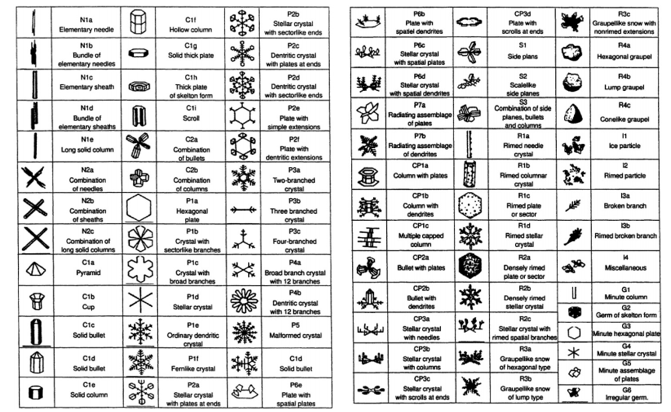
Źródło: H. R. Pruppacher, J. D. Klett, Microphysics of Clouds and Precipitation , Second edition, Springer Dordrecht, 2010
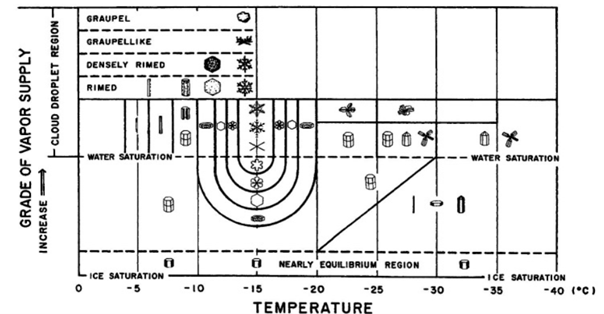
Źródło: H. R. Pruppacher, J. D. Klett, Microphysics of Clouds and Precipitation , Second edition, Springer Dordrecht, 2010
To jaki kryształ powstanie zależy między innymi od temperatury oraz od stanu przesycenia powietrza.
Z punktu widzenia zjawiska halo istotne są dwa rodzaje kryształków lodu.
A mianowicie kryształ, który nazywany jest ołówkowym (dlatego ponieważ wyglądem przypomina niezaostrzony ołówek), czy też inaczej słupkowym oraz płytkowy.
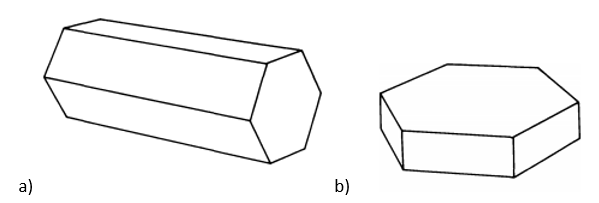
Kryształki istotne z punktu widzenia tworzenia halo, a) kryształek słupkowy (ołówkowy) (C1e), b) kryształek płytkowy (P1a).
Źródło: Robert Greenler, Tęcze, glorie i halo, wyd. Prószyński i S-ka, 1999.
Kiedy promienie świetlne padają na jedną ze ścian kryształu, ulegają załamaniu. Następnie światło porusza się w ośrodku lodowym, aż na swojej drodze napotyka płaszczyznę drugiej ściany i ponownie ulegnie załamaniu. Ponieważ współczynnik załamania zależy od długości fali, dlatego podczas pierwszego, a następnie podczas drugiego załamania światło ulega rozszczepieniu. Przypomnijmy sobie doświadczenie z optyki, którego świadkami był każdy z nas na lekcji fizyki. Kiedy pryzmat trójkątny został oświetlony wiązką światła na ekranie otrzymano kolorowe pasmo światło.
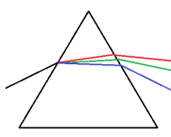
Podobne zjawisko zachodzi kiedy światło pada na kryształ słupkowy lub płytkę. Wyobraźmy sobie, że co drugą ścianę kryształu rozciągamy. W wyniku tego zabiegu otrzymujemy bryłę lodową, która w przekroju przypominać będzie pryzmat trójkątny.
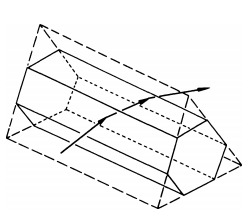
Źródło: Robert Greenler, Tęcze, glorie i halo, wyd. Prószyński i S-ka, 1999.
Przebieg promienia świetlnego w takiej bryle będzie dokładnie taka sami jak w pryzmacie obserwowanym na lekcjach fizyki. Z optyki geometrycznej wiadomo, że kierunki promienia padającego na kryształ i z niego wychodzące nie są takie same. Wychodzący promień odchyla się o pewien kąt. Obracając kryształem wokół osi prostopadłej do kierunku padającego promienia słonecznego spostrzeżemy, że kąt odchylenia się zmienia. Jeżeli zaczniemy obracać kryształem zgodnie z kierunkiem ruchu wskazówek zegara, to zauważymy, że wartość kąta zawartego między promieniem wchodzącym do kryształu, a promieniem z niego wychodzącym maleje osiągając wartość najmniejszą, a następnie zaczyna ponownie wzrastać. Obracając kryształem w kierunku przeciwnym zaobserwujemy identyczny efekt. Można zadać pytanie jakie muszą być spełnione warunki, aby kąt odchylenia promienia słonecznego po przejściu przez pryzmat był najmniejszy. Otóż kąt osiągnie wartość minimalną tylko podczas symetrycznego rozkładu promienia padającego na kryształ i promienia wychodzącego. Wartość kąta minimalnego odchylenia zależy od właściwości optycznych ośrodka (od współczynnika załamania ośrodka, w naszym wypadku lodu) oraz od kąta łamiącego pryzmatu.
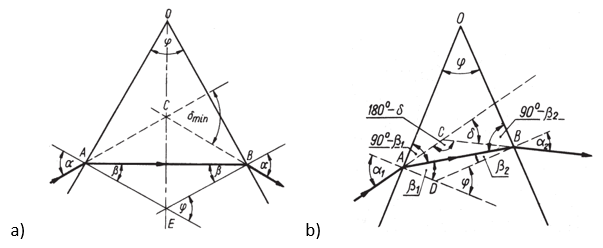
Źródło: Z. Kamiński, W. Kamiński, Fizyka dla kandydatów na wyższe uczelnie techniczne, tom 2, PWN, 2018.
Dla pozostałych ustawień kryształu kąt δ jest większy od wartości minimalnej δ > δmin.
Wartość kąta odchylenia można wyznaczyć korzystając z elementarnej geometrii:
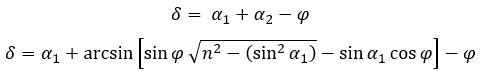
gdzie: α1 kąt padania (kąt zawarty między normalną do powierzchni na którą pada promień światła, a kierunkiem promienia świetlnego), α2 kąt załamania (kąt zawarty między normalną do drugiej powierzchni, na którą pada promień światła, a kierunkiem promienia świetlnego wychodzącego z bryły lodu), φ kąt łamiący pryzmatu.
Kąt odchylenia osiąga wartość minimalną przy symetrycznym przejściu promienia (kąty α1 = α2 = α) przez pryzmat i wynosi:
δmin = 2α – φ
Wartość kąta najmniejszego odchylenia promienia świetlnego po przejściu przez pryzmat można wyznaczyć, jeśli znamy współczynnik załamania światła oraz kąt łamiący pryzmatu:
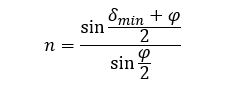
zatem:
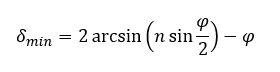
Prześledźmy dokładnie ruch promienia świetlnego w lodowym krysztale. Są dwie możliwości. Jeżeli promienie słoneczne padają na kryształ płytkowy lub ołówkowy, którego dwie ściany tworzą ze sobą kąt wynoszący dokładnie 60° (kąt łamiący lodowego pryzmatu), to kąt najmniejszego odchylenia wyniesie 22° (a dokładnie 21°54′), czyli tyle ile wynosi promień kątowy pierścienia wokół Słońca. Współczynnik załamania zależy od długości fali. Im większa długość fali tym współczynnik załamania jest mniejszy. W kryształkach lodu współczynnik załamania światła o długości barwy fioletowej wynosi nf=1,317, natomiast dla światła o długości fali czerwonej wynosi nc=1,307.
Ponieważ współczynnik załamania dla fali czerwonej jest mniejszy, zatem minimalny kąt odchylenia będzie mniejszy w porównaniu z kątem minimalnego odchylenia dla promienienia niebieskiego, dla którego współczynnik załamania jest większy. Zatem wewnętrzny promień kątowy pierścienia halo koloru czerwonego wynosi 21°36′, zaś promień kątowy pierścienia zewnętrznego (niebieskiego) wynosi 22°22′.
W sytuacji kiedy ściany kryształu graniastosłupa tworzą kąt 90°, to najmniejszy kąt jaki jest zawarty między kierunkiem promienia padającego, a promieniem załamanym wynosi 46° (a dokładnie 45°44′), czyli tyle ile wynosi promień kątowy pierścienia wokół Słońca (większe halo). Wewnętrzny promień kątowy pierścienia halo koloru czerwonego wynosi 45° zaś promień kątowy pierścienia zewnętrznego (koloru fioletowego) wynosi 47°14′. Zjawisko 46° halo występuję sporadycznie i stanowi około 2 % wszystkich zdarzeń [6].
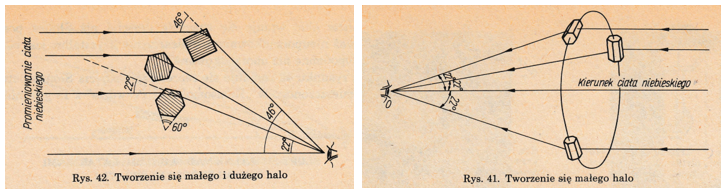
Źródło: W. Bułat. Zjawiska optyczne w przyrodzie. Wyd. WSiP, 1978
Jest jeszcze jedna para ścian w krysztale, które tworzą ze sobą kąt 120°, są to ściany bezpośrednio sąsiadujące ze sobą. Ta para ścian, nie odgrywa jednak żadnej roli z punktu widzenia halo. Promień świetlny wchodząc do bryły lodu przez płaszczyznę jednej ściany ma możliwość jedynie całkowitego wewnętrznego odbicia się od wewnętrznej płaszczyzny drugiej ściany sąsiadującej, czyli promień światła nie wychodzi z kryształu.
Kryształki lodu znajdujące się w atmosferze rozmieszczone są chaotycznie. Promienie światła padając na kryształki mogą ulegać podwójnemu załamaniu (promienie 1, 3, 5, 7) lub podwójnemu załamaniu i jednokrotnemu odbiciu (promienie 2, 4, 6) [4].
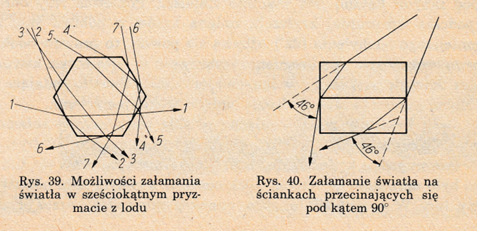
Źródło: W. Bułat. Zjawiska optyczne w przyrodzie. Wyd. WSiP, 1978
Promienie mogą wychodzić z kryształków pod różnymi kątami. Kiedy przeprowadzimy analizę matematyczną natężenia światła w funkcji kąta odchylenia promienia świetlnego wychodzącego z kryształu to okazuje się, że natężenie uzyskuje największą wartość dla kąta najmniejszego odchylenia, a więc natężenie światła dla promieni odchylających się minimalnie jest największe i dlatego obserwator ma możliwość obserwacji kolorowych okręgów wokół Słońca lub białych wokół Księżyca o promieniach kątowych, których wartości zostały wcześniej podane. Natężenie światła dla promieni wychodzących pod innym kątem jest znacząco mniejsze i promienie te mogą tworzyć aureolę wokół głównego kręgu halo.
Zjawisko halo najłatwiej jest obserwować gdy występują duże kryształy. W wypadku kiedy rozmiary kryształu maleją, maleje również intensywność halo [6].
Zjawisko halo może być zaobserwowane przez obserwatora znajdującego się na powierzchni ziemi. Czasami chmura jest na tyle gruba, że z powierzchni ziemi nie można zobaczyć zjawiska, dopiero będąc wewnątrz chmury ukazuje się piękne zjawisko optyczne. Lecąc samolotem i obserwując chmury z pewnej wysokości również można zaobserwować piękne zjawiska optyczne. Przeanalizujemy to z różnej perspektywy obserwatora [2].
Obserwator na powierzchni Ziemi.
Zjawisko halo można zaobserwować na następujących rodzajach chmur:
a) Cirrus
Chmury Cirrus zbudowane są z kryształków lodu zatem na chmurze można obserwować zjawisko halo. Ponieważ występują na niebie w postaci ławic lub wąskich pasm i są małych rozmiarów, zjawisko halo nigdy nie występuje w postaci pełnych kręgów.
b) Cirrostratus
Chmury Cirrostratus podobnie jak Cirrus zbudowana jest z kryształków lodu i jest to chmura znacznych rozmiarów pokrywająca niebo częściowo lub całkowicie. Halo można podziwiać w postaci pełnych kręgów. W wypadku kiedy chmury Cirrostratus są bardzo cienkie i są nieuchwytne naziemnym obserwacją wówczas halo jest jedynym wskaźnikiem ich obecności na niebie.
c) Stratocumulus
Z chmur Stratocumulus mogą wypadać obfite ilości kryształki lodu, które tworzą virga. Promienie światła natrafiając na kryształki lodu tworzących virga tworzą zjawisko halo.
d) Stratus
W bardzo niskich temperaturach chmury Stratus mogą być zbudowane z małych kryształków lodu. Takie lodowe chmury Stratus są na ogół cienką warstwą, a kryształki z których są zbudowane mogą tworzyć zjawisko halo.
Obserwator znajdujący się będący wewnątrz chmury:
a) Cirrus
Ponieważ chmura Cirrus zbudowana jest wyłącznie z kryształków lodu, obserwator który znajdzie się w jej wnętrzu będzie mógł obserwować zjawisko halo w postaci małego kręgu.
b) Cirrocumulus
Chmury Cirrocumulus również zbudowana jest z kryształków lodu oraz mogą wystąpić przechłodzone kropelki wody, które jednak bardzo szybko przekształcają się w kryształki lodu. Obserwator wewnątrz chmury Cirrocumulus również zaobserwuje zjawisko halo w postaci małych kręgów.
c) Cirrostratus
Cirrostratus podobnie jak pozostałe chmury pierzaste zbudowane są z kryształków lodu. Będąc w tej chmurze również zaobserwujemy zjawisko halo i to każdego rodzaju.
d) Altostratus
Wewnątrz jednorodnej chmury Altostratus również można zaobserwować zjawisko halo, często bardzo jasne.
Obserwator znajdujący się powyżej chmury:
a) Cirrostratus
Obserwując chmurę z góry można zaobserwować halo, jednakże zjawisko występuje dość rzadko.
Literatura
- Międzynarodowy Atlas Chmur – atlas skrócony, wydawnictwo Geologiczne, IMGW, 1987, na podstawie wydania z 1956.
- International Cloud Atlas, Volume I, Revised edition 1975, Manual on the observation of clouds and other meteors, WMO-No. 407, 1975
- Robert Greenler, Tęcze, glorie i halo, wyd. Prószyński i S-ka, 1999.
- W. Bułat. Zjawiska optyczne w przyrodzie. Wyd. WSiP, 1978
- Z. Kamiński, W. Kamiński, Fizyka dla kandydatów na wyższe uczelnie techniczne, tom 2, PWN, 2018
- A. A. Kokhanovsky, Cloud Optics, Springer, 2006.
- H. R. Pruppacher, J. D. Klett, Microphysics of Clouds and Precipitation , Second edition, Springer Dordrecht, 2010.
