SŁOWNIK DLA MEDIÓW
NAJWAŻNIEJSZE POJĘCIA I ZWROTY
W MODELOWANIU METEOROLOGICZNYM
Opracowali: Bogdan Bochenek, Mariusz Figurski, Marta Gruszczyńska, Alan Mandal, Jan Szturc, Andrzej Wyszogrodzki i Michał Ziemiański, LMM IMGW-PIB
DEFINICJE KLUCZOWE
Prognoza ogólnego charakteru pogody
Prognoza długoterminowa
Prognoza długoterminowa – szczegółowa
Prognoza długoterminowa – tygodniowa
Prognoza długoterminowa – dekadowa
Prognoza długoterminowa – miesięczna
Prognoza długoterminowa – sezonowa
Norma (prognozy długoterminowe)
Prognoza nowcastingowa
Prognoza ultra-krótkoterminowa
Prognoza numeryczna
Numeryczne modele pogody
Rozdzielczość numerycznych modeli pogody
Generalna charakterystyka numerycznych modeli pogody
WPROWADZENIE
Niniejszy słownik zawiera definicje najważniejszych pojęć stosowanych w dziedzinie modelowania meteorologicznego oraz prognozowania długoterminowego. Wybrane pojęcia z dziedziny modelowania przedstawiają podstawową charakterystykę warsztatu modelowania pogody, w tym numerycznego. Pojęcia te definiują główne cechy charakterystyczne stosowanych operacyjnie modeli pogody. Przedstawione definicje mają pomóc użytkownikowi prognoz modelowych w zrozumieniu ich natury oraz ułatwić porównanie charakterystyk poszczególnych modeli stosowanych operacyjnie w IMGW-PIB. Pojęcia z dziedziny prognozowania długoterminowego informują ich użytkowników o poszczególnych klasach takich prognoz i ich podstawowych charakterystykach.
Słownik podzielony jest na dwie części. Część pierwsza zawiera kluczowe definicje dotyczące prognoz długoterminowych oraz ogólne definicje najbardziej podstawowych pojęć związanych z modelowaniem pogody. Część druga zawiera definicje szczegółowe, które rozwijają definicje kluczowe oraz przedstawiają charakterystyki poszczególnych modeli stosowanych operacyjnie w IMGW-PIB. Na końcu opracowania umieszczono alfabetyczny indeks haseł, aby ułatwić korzystanie ze Słownika. Używane definicje pochodzą głównie z literatury naukowej dotyczącej modelowania numerycznego oraz statystycznego. Jest ona bardzo obszerna i na końcu Słownika przedstawiono kilka wybranych pozycji.
DEFINICJE KLUCZOWE
(I) PROGNOZA OGÓLNEGO CHARAKTERU POGODY
Stosowana głównie na potrzeby prognoz długoterminowych. W przeciwieństwie do prognozy pogody, nie zawiera szczegółowych informacji o pogodzie na dany dzień, a jedynie ogólne informacje o trendach, jakie mogą wystąpić w dłuższym okresie czasu, najczęściej tygodnia, miesiąca lub sezonu. Za pomocą takich parametrów, jak np. średnia temperatura powietrza lub suma opadów atmosferycznych, przewiduje się czy prognozowany okres (tydzień, miesiąc, sezon) będzie cieplejszy, chłodniejszy, bardziej suchy, lub bardziej wilgotny niż normalnie. Patrz: norma (prognozy długoterminowe).
(II) PROGNOZA DŁUGOTERMINOWA
Prognoza pogody lub prognoza ogólnego charakteru pogody na co najmniej 14 dni do przodu. Prognozy długoterminowe dzielimy na prognozy: szczegółowe, tygodniowe, dekadowe, miesięczne, sezonowe.
(III) PROGNOZA DŁUGOTERMINOWA – SZCZEGÓŁOWA
Prognoza pogody na każdy dzień tygodnia na co najmniej 14 dni do przodu; najczęściej na 14-15 dni do przodu, np. prognoza numeryczna modelu WRF-GFS Medium.
(IV) PROGNOZA DŁUGOTERMINOWA – TYGODNIOWA
Prognoza ogólnego charakteru pogody na każdy tydzień kalendarzowy na co najmniej 2 tygodnie do przodu; najczęściej na 4-6 tygodni do przodu, np. prognoza numeryczna modelu ECMWF EPS 46.
(V) PROGNOZA DŁUGOTERMINOWA – DEKADOWA
Prognoza ogólnego charakteru pogody na każdą dekadę miesiąca (okres 10 dni) na co najmniej 2 dekady do przodu; najczęściej na 3 dekady do przodu, np. prognoza numeryczno-statystyczna modelu IMGW-TWS.
(VI) PROGNOZA DŁUGOTERMINOWA – MIESIĘCZNA
Prognoza ogólnego charakteru pogody na dany miesiąc kalendarzowy na co najmniej 1 miesiąc do przodu; najczęściej na 3-6 miesięcy do przodu, np. eksperymentalna prognoza długoterminowa temperatury i opadu na 4 miesiące IMGW-PIB lub prognoza numeryczna modelu CFS.
(VII) PROGNOZA DŁUGOTERMINOWA – SEZONOWA
Prognoza ogólnego charakteru pogody na dany sezon kalendarzowy (okres 3 miesięcy) na co najmniej 3 miesiące do przodu.
(VIII) NORMA (PROGNOZY DŁUGOTERMINOWE)
Stosowana najczęściej na potrzeby prognoz ogólnego charakteru pogody w prognozach długoterminowych – miesięcznych. Prognozowaną średnią miesięczną temperaturę powietrza/miesięczną sumę opadów atmosferycznych dla danego miesiąca przewiduje się w odniesieniu do normy wieloletniej przyjmowanej za okres 1991-2020. Wartości średniej miesięcznej temperatury/miesięcznej sumy opadów z tego 30-letniego okresu sortuje się od najniższej do najwyższej: 10 najniższych wartości wyznacza średnią temperaturę/sumę opadów w klasie „poniżej normy”, 10 środkowych „w normie”, a 10 najwyższych „powyżej normy”. Gdy przewidywana jest średnia temperatura/suma opadów:
- powyżej normy, przewiduje się, że prognozowany miesiąc będzie cieplejszy/bardziej mokry od co najmniej 20 obserwowanych, tych samych miesięcy w latach 1991-2020;
- poniżej normy, przewiduje się, że prognozowany miesiąc będzie chłodniejszy/bardziej suchy od co najmniej 20 obserwowanych, tych samych miesięcy w latach 1991-2020;
- w normie, przewiduje się, że prognozowany miesiąc będzie podobny do typowych 10 obserwowanych, czyli cieplejszy/bardziej mokry od co najmniej 10 obserwowanych i chłodniejszy/bardziej suchy od co najmniej 10 obserwowanych, tych samych miesięcy w latach 1991-2020.
Uwaga: Normę stosowaną w prognozach długoterminowych IMGW-PIB nie należy mylić z normą stosowaną w analizach klimatologicznych IMGW-PIB. Patrz: norma (analizy klimatologiczne).
(IX) PROGNOZA NOWCASTINGOWA
Prognoza tworzona przez modele nowcastingowe, których cechą jest wysoka rozdzielczość czasowa i przestrzenna (odpowiednio rzędu 5-10 min i 1 km) oraz duża sprawdzalność dla krótkich czasów wyprzedzenia – do ok. 2 godz. dla pola opadu i do ok. 6 godz. w przypadku pozostałych pól meteorologicznych. Najczęściej stosuje się podejście ekstrapolacyjne, polegające na precyzyjnej estymacji warunków początkowych, ich ekstrapolacji w oparciu o obliczone wektory przemieszczania się, oraz ewolucji w czasie. Inne podejście polega na korekcie prognoz z modeli mezoskalowych danymi pomiarowymi, stosowane najczęściej do pól meteorologicznych innych niż opad.
(X) PROGNOZA ULTRA-KRÓTKOTERMINOWA
Prognoza na okres do 12 (maksymalnie 18) godzin. Zwykle są to prognozy realizowane przez modele numerycznych prognoz pogody asymilujące bieżące dane pomiarowe i obserwacyjne.
(XI) PROGNOZA NUMERYCZNA
Prognoza numeryczna przedstawia przyszły stan atmosfery obliczony za pomocą numerycznych modeli pogody. Jej treść publikowana jest bez ingerencji lub weryfikacji przez człowieka (np. synoptyka meteorologa). Prognozy te mają zwykle formę graficzną. Najczęściej stosowane są mapy rozkładu poszczególnych parametrów meteorologicznych przy powierzchni ziemi lub w górnej atmosferze (na powierzchniach stałego ciśnienia, czyli izobarycznych), dla wybranych chwil. Mogą to być także przekroje pionowe ukazujące przestrzenny rozkład wybranych parametrów meteorologicznych. Szczególną formą są tzw. meteogramy przedstawiające prognozowaną ewolucję wybranych parametrów meteorologicznych dla określonego miejsca (wybranej miejscowości). Prognozy numeryczne są jedną z podstaw do opracowania prognozy synoptycznej.
(XII) NUMERYCZNE MODELE POGODY
Numeryczne modele pogody są zaawansowanymi programami komputerowymi, które rozwiązują równania fizyki, opisujące w sposób matematyczny, jak stan pogody i atmosfery zmienia się w czasie i przestrzeni. Rozwiązania te są przybliżone i obliczane tylko dla poszczególnych, oddalonych od siebie, „węzłów” w 3-wymiarowej przestrzennej sieci obliczeniowej. Przybliżenia są tak konstruowane, aby ich nieuniknione błędy były jak najmniejsze, a twórcy poszczególnych modeli stosują różne matematyczne formy tych przybliżeń.
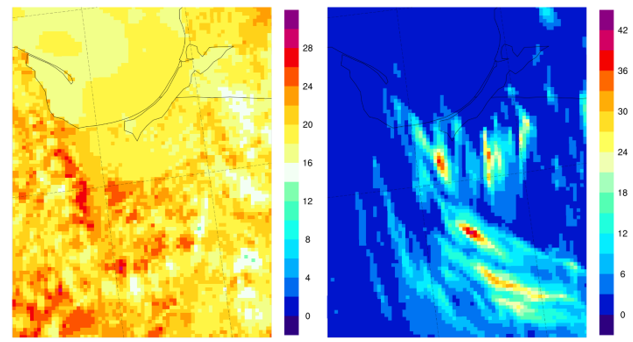
Rysunek ilustruje poziomą konfigurację numerycznej siatki obliczeniowej modelu COSMO-EULAG na przykładzie prognozy temperatury na wysokości 2 m nad ziemią (stopnie C, lewy panel) oraz skumulowanego opadu (mm, prawy panel) dla fragmentu północnej Polski na 11 lipca 2022, godz. 1200 UTC. Rozmiar pikseli rastra odpowiada rozmiarowi oczka siatki obliczeniowej,
a jej węzły znajdują się w środku poszczególnych pikseli rastra. Pozioma odległość
między sąsiednimi węzłami siatki numerycznej wynosi 2,2 km.
(XIII) ROZDZIELCZOŚĆ NUMERYCZNYCH MODELI POGODY
Dokładność prognoz numerycznych zależy m.in. od gęstości sieci obliczeniowej modelu pogody, czyli od odległości pomiędzy jej sąsiednimi węzłami: im mniejsza odległość, tym gęstsza sieć i lepsze przybliżenie. Gęstość sieci numerycznej zależy od mocy obliczeniowej stosowanych superkomputerów. Im większa moc, tym więcej operacji można wykonać w ograniczonym czasie przeznaczonym na obliczenie prognozy, a więc tym więcej węzłów może zawierać sieć obliczeniowa modelu i tym mniejsza może być odległość pomiędzy nimi. Obecnie poziome odległości pomiędzy sąsiednimi węzłami osiągnęły około 10 km (lub nieco więcej) w modelach globalnych i kilka kilometrów w modelach regionalnych. Pionowe odległości pomiędzy sąsiednimi węzłami zmieniają się z wysokością – od kilkudziesięciu metrów przy powierzchni podłoża do kilkuset metrów w głębi atmosfery.
W terminologii naukowej przez rozdzielczość modelu rozumie się przestrzenny rozmiar najmniejszego obiektu meteorologicznego, którego ewolucja może być poprawnie przedstawiona przez ten model. Rozmiar ten jest około 6 do 8 razy większy niż pozioma odległość pomiędzy sąsiednimi węzłami sieci obliczeniowej.
W stosowanej najczęściej terminologii potocznej przez rozdzielczość modelu rozumie się po prostu poziomą odległość pomiędzy sąsiednimi węzłami jego sieci obliczeniowej. W praktyce warto doprecyzować, które z tych dwu znaczeń stosowane jest w danym stwierdzeniu.
(XIV) GENERALNA CHARAKTERYSTYKA NUMERYCZNYCH MODELI POGODY
W działaniu numerycznych modeli pogody możemy wyróżnić szereg funkcjonalności, które są niezbędne dla obliczenia wiarygodnej prognozy pogody. I tak, podstawową częścią modelu jest tzw. rdzeń dynamiczny. Jest to ta część kodu modelu, która praktycznie rozwiązuje prognostyczne równania fizyki, opisujące ewolucję stanu atmosfery, na obliczeniowej sieci modelu. Numeryczne modele pogody muszą jednak uwzględnić fakt, że poszczególne procesy atmosferyczne odbywają się w obszarach o różnych wielkościach. Niektóre procesy mają miejsce w tak małych objętościach atmosfery, że nie mogą być bezpośrednio odwzorowane na sieci obliczeniowej modelu. Procesy takie nazywamy podskalowymi. Przykładem są oddziaływania mikrofizyczne związane z kondensacją pary wodnej oraz tworzeniem chmur i opadów, które odbywają się w skalach centymetrowych, a nawet mniejszych. Modele pogody obliczają przybliżone efekty takich procesów za pomocą specjalnych procedur zwanych parametryzacjami. Przybliżają one sumaryczny efekt procesu, zagregowany dla całego oczka sieci obliczeniowej modelu. Poszczególne modele pogody stosują różne metody parametryzacji poszczególnych procesów podskalowych. Dalej, obliczenia prognostyczne muszą uwzględnić istotną rolę procesów wymiany ciepła i wody pomiędzy atmosferą a podłożem. Do tego celu wykorzystuje się dodatkowe specjalne modele, które obliczają ewolucję stanu podłoża oraz wielkość tej wymiany, w zależności od prognozowanej sytuacji meteorologicznej.
Procedury modelu mogą rozpocząć obliczanie prognozy pod warunkiem dostarczenia im informacji o stanie atmosfery w momencie, który jest początkiem okresu prognostycznego. Informacja ta (tzw. warunki początkowe) musi być zadana we wszystkich węzłach 3-wymiarowej sieci obliczeniowej, a dla wiarygodnej prognozy powinna być jak najbliższa rzeczywistemu stanowi atmosfery w tym momencie. Wymagane wartości poszczególnych parametrów meteorologicznych obliczane są przez specjalne procedury na podstawie wyników bieżących obserwacji i pomiarów meteorologicznych (przyziemnych, balonowych, satelitarnych, etc.) oraz wyników prognoz (zwykle kilkugodzinnych) samego modelu. Procedury te nazywamy procedurami asymilacji danych obserwacyjnych.
Numeryczne modele pogody są zatem niezwykle złożonymi systemami. Są one ciągle rozwijane tak, aby wykorzystywać w nich bieżące postępy w wielu różnych dziedzinach nauki. Dotyczy to zarówno nauk podstawowych, od matematyki z metodami numerycznymi oraz statystycznymi po fizykę procesów atmosferycznych i procesów w środowisku naturalnym, jak i informatyki oraz inżynierii – od komputerowej po pomiarową.
DEFINICJE SZCZEGÓŁOWE
(1) Konsorcja numerycznego modelowania pogody – konsorcja, których członkami są narodowe służby meteorologiczne lub hydrologiczno-meteorologiczne, i których celem jest rozwijanie i doskonalenie narzędzi do prowadzenia numerycznych prognoz pogody, w tym modeli numerycznych, systemów asymilacji danych i weryfikacji prognoz. W Europie działa kilka takich konsorcjów i są to: ACCORD (A Consortium for Convection-scale modelling Research and Development, powstały z połączenia konsorcjów ALADIN i HIRLAM), COSMO (Consortium for Small-Scale Modeling) i RC LACE (Regional Cooperation for Limited Area modeling in Central Europe). IMGW-PIB jest członkiem wszystkich tych konsorcjów.
(2) Model ALARO (ALADIN and AROME) – jeden z numerycznych modeli pogody systemu ALADIN, rozwijany głównie przez kraje grupy RC LACE. Fizyka modelu ALARO zdefiniowana jest w ten sposób, aby mogła z powodzeniem przewidywać pogodę w skalach tzw. „szarej strefy”, czyli pomiędzy prognozami mezoskalowymi a skalami pozwalającymi na rozwiązywanie problemów konwekcyjnych. Model ALARO wykorzystywany jest operacyjnie przez wiele krajów konsorcjów ALADIN i HIRLAM w prognozach deterministycznych, probabilistycznych i badaniach klimatu. W IMGW-PIB działa operacyjnie od 2014 roku na siatce o rozdzielczości przestrzennej 4 km i 70 poziomach wertykalnych. Prognozy liczone są 4 razy dziennie do 72 godzin.
(3) Model AROME (Application de la Recherche a l’Operationnel a Meso-Echelle) – jeden z numerycznych modeli pogody systemu ALADIN, rozwijany głównie przez Meteo France. Ma na celu prognozowanie pogody na siatkach o rozdzielczościach poniżej 2,5 km. Wykorzystywany jest z powodzeniem na całym świeci i służy prognozom groźnych zjawisk pogodowych, badaniom klimatu i coraz częściej jako model nowcastinowych, uruchamiany w systemach typu RUC (Rapid Update Cycle) w domenach o rozdzielczościach przestrzennych rzędu 1 km. W IMGW-PIB działa operacyjnie od 2015 roku na siatce o rozdzielczości przestrzennej 2 km i 70 poziomach wertykalnych. Prognozy liczone są 4 razy dziennie na 30 godzin.
(4) Model burzowy TSP (Thunderstorm Prediction) – nowcastingowy model TSP służy do detekcji burz i określania ich intensywności oraz prawdopodobieństwa wystąpienia, a także do prognozowania tych wielkości co 10 min, z czasem wyprzedzenia do 1 godz., z 1-km rozdzielczością przestrzenną. Dane wejściowe do modelu pochodzą z następujących systemów pomiarowych: PERUN (przetworzone modelem LIGHTNING, w tym pole lightning jump), sieć radarowa POLRAD (w postaci różnych tzw. produktów) oraz sieć satelitów Meteosat (przetworzone oprogramowaniem EUMETSAT NWC-SAF). W modelu TSP wykorzystano algorytm SVM (ang. support vector machines) do detekcji burz i klasyfikowania ich intensywności oraz do prognozowania ich dalszego rozwoju. Do prognozowania przemieszczania się poszczególnych komórek burzowych wykorzystuje się pola wektorów z modelu nowcastingowego SCENE.
(5) Model COSMO (Consortium for Small-Scale Modeling) – mezoskalowy model meteorologiczny rozwijany w ramach międzynarodowej współpracy konsorcjum COSMO, do którego IMGW-PIB należy od roku 2003. Model ten wykorzystuje system analizy i asymilacji danych pomiarowych, pozwalający na poprawę warunków początkowych prognozy, dostarczanych z modelu globalnego ICON (liczonego w DWD). Wyniki modelu wykorzystywane są jako dane wejściowe do modeli hydrologicznych opad–odpływ, modeli nowcastingu i falowania oraz służą zespołom synoptyków do przygotowania codziennych prognoz, ostrzeżeń i komunikatów pogodowych. Model COSMO uruchamiany jest w IMGW-PIB cztery razy na dobę w terminach 00, 06, 12, 18 UTC, na siatkach o dwóch rozdzielczościach horyzontalnych. Prognozy na siatce 7 km, pokrywające centralną część Europy i cały obszar Morza Bałtyckiego, wykonywane są z wyprzedzeniem do 78 godzin. Prognozy na gęstszej siatce o rozdzielczości 2,8 km, pokrywające obszar Polski i część powierzchni krajów ościennych, mają wyprzedzenie do 48 godzin.
(6) Model estymacji pola opadu (RainGRS) – system RainGRS generuje estymowane pola opadu z wysoką rozdzielczością czasową i przestrzenną (10 min, 1 km). Wejściem są dane dostarczane przez różne techniki pomiarowe: sieć deszczomierzową IMGW-PIB, sieć radarową POLRAD uzupełnioną o dane z radarów zagranicznych, oraz pomiary satelitarne Meteosat. Wszystkie dane są weryfikowane i korygowane dedykowanymi algorytmami. Łączenie poszczególnych danych wejściowych odbywa się za pomocą algorytmu kombinacji warunkowej, uwzględniającego także ilościową informację o rozkładzie przestrzennym ich jakości.
(7) Model ECMWF EPS 46 – model oparty na operacyjnych danych prognostycznych Europejskiego Centrum Prognoz Średnioterminowych (European Centre for Medium-Range Weather Forecast, ECMWF), które IMGW-PIB otrzymuje na bieżąco dzięki umowie zawartej w 2020 roku. Model ECMWF EPS 46 dostarcza 2 razy w tygodniu prognozę temperatury powietrza i opadu na następne 46 dni, w postaci tygodniowych rozwiązań. Prognozowane parametry pozyskuje się z 50 realizacji tego samego wyprzedzenia, różniących się między sobą parametryzacją (tzw. prognoza wiązkowa).
(8) Model INCA-PL2 – system INCA-PL2 przeznaczony do prognoz nowcastingowych podstawowych pól meteorologicznych poza opadem; jest zmodyfikowaną wersją modelu INCA opracowanego przez austriacką służbę meteorologiczną (ZAMG). Prognozy te są generowane na podstawie pól prognostycznych z modelu mezoskalowego AROME oraz aktualnych pomiarów telemetrycznych, przy uwzględnieniu wpływu orografii terenu. Dla danych bieżących stosowany jest 10-min krok czasowy. Dla prognoz stosowany jest 1-godz. krok czasowy, z takim krokiem są one również uaktualniane, przy czym ich czas wyprzedzenia wynosi do 8 godz. Rozdzielczość przestrzenna wszystkich produktów INCA-PL2 wynosi 1 km.
(9) Model opadu MERGE – system MERGE produkuje prognozy hybrydowe opadu całkowitego i opadu śniegu. Łączone są prognozy nowcastingowe, generowane przez model SCENE, z prognozami mezoskalowymi z modelu AROME. Prognoza powstaje przez zastosowanie funkcji wagowej nadającej różne wagi tym dwóm prognozom; przy krótszych czasach wyprzedzenia większą wagę mają prognozy SCENE. Krok czasowy prognoz wynosi 10 min, a czas wyprzedzenia do 8 godz., przy zachowaniu wysokiej, 1-km rozdzielczości przestrzennej. Prognozy są uaktualniane co 10 minut.
(10) Model WRF METEOPG – prognostyczny system pogodowy, operacyjnie pracujący i rozwijany od 2018 roku w Centrum Informatycznym TASK na Politechnice Gdańskiej przez zespół prof. Mariusza Figurskiego z Katedry Geodezji Wydziału Inżynierii Lądowej i Środowiska PG, który wykorzystuje niehydrostatyczny model WRF (Weather Research and Forecasting). Prognozy z WRF METEOPG udostępniane są do IMGW-PIB na mocy podpisanego porozumienia o współpracy między Politechniką Gdańską i Instytutem Meteorologii i Gospodarki Wodnej z 2019 roku. W systemie zastosowano wysokorozdzielcze dane geograficzne (m.in. obejmujące topografię, szorstkość podłoża, użytkownie gruntów) i zoptymalizowaną parametryzacją fizyki dla Europy Środkowej. Operacyjny model wykorzystuje trzy siatki zanurzone o rozdzielczościach odpowiednio 12,5, 2,5 i 0,5 km na 50 wertykalnych hybrydowych poziomach obliczeniowych. Siatka pierwsza obejmuje kontynent europejski, druga obszar Polski, a trzecia województwo pomorskie. W systemie można również aktywować kolejne siatki o rozdzielczości 0,5 km dla wskazanych obszarów Polski, np. Tatr i Podhala. Do prognozowania pogody asymilowane są dane z globalnego modelu GFS (Global Forecast System) o rozdzielczości 0,25°, który zawiera w sobie sprzężone modele atmosfery, gleby i oceanu. Alternatywnie system może asymilować dane z modelu europejskiego ICON-EU (Icosahedral Nonhydrostatic for Europe) o rozdzielczości 6,6 km lub pobierać dane wejściowe z modeli IMGW COSMO (Consortium for Small-Scale Modeling) i ICON-LM oraz ERA5 z ECMWF (European Center for Medium-range Weather Forecast). System WRF METEOPG w ciągu doby uruchamiany jest dla czterech głównych terminów synoptycznych – 00, 06, 12 i 18 – z czasem prognozy wynoszącym 60 godzin dla wszystkich siatek obliczeniowych. System obliczeniowy prognozowania pogody pracuje na superkomputerze “TRYTON” wykorzystując 24 węzły obliczeniowe.
(11) Model WRF ICON – eksperymentalny model opracowany w ramach projektu obliczeniowego w Centrum Informatycznym TASK „Parametryzacja i opracowanie mezoskalowego numerycznego modelu pogody WRF wysokiej rozdzielczości z asymilacją danych meteorologicznych i GNSS”. Model jest implementacją modelu WRF (Weather Research and Forecasting) opracowanego w NCAR. W celu uniknięcia dużego skoku z rozdzielczości danych wejściowych do rozdzielczości modelu, wynoszącej 2,5 km, w implementacji WRF ICON do inicjalizacji i warunków początkowych i bocznych w całości wykorzystywany jest model ICON-EU z siatką 6,5 km; model jest inicjowany przez pobranie 61 poziomów modelu ICON-EU atmosfery i 6 poziomów gleby w trzy godzinnych interwałach. Zapewnia to niezwykle szczegółową inicjalizację, a marginalne błędy domeny są zredukowane do minimum. Implementacja danych początkowych z modelu ICON-EU jest autorskim rozszerzeniem prof. Mariusz Figurskiego, który dokonał przebudowy modelu WRF v4.3 w celu wykorzystania danych początkowych zarówno z modelu ICON-EU, jak również modelu globalnego ICON o rozdzielczości 13 km. Ze względu na nowe rozwiązania w schemacie NOAH-MP WRF v4.3, związane z obliczaniem procesów hydrotermalnych symulujących zachowanie pokrywy śnieżnej na gruncie, oczekiwane jest również lepsze zachowania modelu w warunkach zimowych, gdy grunt jest pokryty śniegiem. Dużą nowością w wersji WRF 4.3 jest inicjalizacja chmur początkowych z wilgotności względnej warunków początkowych, dzięki czemu wyeliminowany został stosunkowo długi okres powstawania chmur i opadów w modelu w okresie rozpędzania modelu. W fazie testów model wykazał znacznie lepsze charakterystyki w symulacji konwekcji, a dzięki zastosowaniu schematu IEVA do sterowania kryterium stabilności pionowej poprawiona została niezawodność numeryczna modelu, a także szybkość symulacji, ponieważ schemat IEVA pozwala na zastosowanie większego maksymalnego kroku czasowego w zastosowaniu adaptacyjnego kroku całkowania, utrzymując stabilność modelu nawet przy wyższych pionowych wartościach CFL. W wersji eksperymentalnej model WRF ICON v4.3 jest uruchamiany raz na dobę dla terminu 00:00, a długość prognozy wynosi 120 godzin.
(12) Model WRF GFS MEDIUM – eksperymentalny model średnioterminowy opracowany w ramach projektu obliczeniowego w Centrum Informatycznym TASK „Parametryzacja i opracowanie mezoskalowego numerycznego modelu pogody WRF wysokiej rozdzielczości z asymilacją danych meteorologicznych i GNSS”. Model jest implementacją modelu WRF (Weather Research and Forecasting) opracowanego w NCAR. Model WRF GFS MEDIUM do zdefiniowania warunków początkowych i bocznych wykorzystuje model GFS v16. Prognoza jest realizowana na dwóch zagnieżdżonych domenach ze sprzężeniem zwrotnym, o rozdzielczościach horyzontalnych odpowiednio 12 km (Europa) i 4 km Polska oraz 50 poziomach wertykalnych. Do zwiększenia prędkości symulacji w modelu WRF GFS MEDIUM zastosowano całkowanie z adaptacyjnym krokiem całkowania. Wprowadzono rozszerzenie dotyczące asymilacji pól hydrometeorów dostępnych w modelu GFS v16, polepszające prognozowanie pól opadowych. Model jest inicjalizowany przez pobranie 34 pól ciśnieniowych oraz 4 poziomów gleby z modelu globalnego GFS v16. Parametryzacja modelu jest identyczna z parametryzacją modelu WRF ICON. W wersji eksperymentalnej model jest uruchamiany raz na dobę dla terminu 12:00, a długość prognozy wynosi 384 godziny.
(13) Numeryczne modele prognoz pogody (ang. Numerical Weather Prediction/NWP) – zaawansowane programy komputerowe, rozwiązujące równania fizyki, które w sposób matematyczny opisują zmiany stanu pogody i atmosfery zachodzące w czasie i przestrzeni. W zależności od zastosowania, modele NWP wykorzystują różne zestawy równań różniczkowych, w których procesy fizyczne opisane są w sposób możliwie najdokładniejszy. Podstawowy układ równań stosowany w modelach NWP to równania Naviera-Stokesa opisujące zasadę zachowania pędu dla poruszającego się płynu, uwzględniające siły masowe, ciśnienie oraz siły lepkości. Równania prognostyczne opisujące zmiany dynamiczne, czyli ewolucję stanu atmosfery, nazywamy równaniami ruchu, a kod numeryczny, który rozwiązuje te równania – rdzeniem dynamicznym modelu.
(14) Metody numeryczne – ze względu na złożoność procesów zachodzących w atmosferze, nie jest możliwe znalezienie analitycznej formy rozwiązań równań opisujących stan pogody. Z tego powodu operatory różniczkowe i całkowe równań są wyrażone w postaci numerycznej na dyskretnej siatce obliczeniowej, a rozwiązanie jest poszukiwane przy pomocy superkomputerów. Rozwój odpowiednich metod i algorytmów numerycznych jest prowadzony w ramach dziedziny nauki zwanej obliczeniową mechaniką płynów (ang, Computational Fluid Dynamics, CFD).
(16) Struktura siatki obliczeniowej – ze względu na charakter ziemskiej atmosfery (stratyfikacja termiczna, transfer promieniowania, topografia) siatka obliczeniowa konstruowana jest inaczej w kierunku poziomym i inaczej w pionowym. W kierunku poziomym siatki mogą być strukturalne (o ustalonych) lub niestrukturalne (o dowolnych powiązaniach między węzłami). W szczególnym przypadku, w którym elementy siatki są przylegającymi do siebie sześcianami, mamy do czynienia z tzw. siatką kartezjańską. W prognozach globalnych, w których ważne jest równomierne pokrycie całej kuli ziemskiej, wykorzystuje się najczęściej siatki trójkątne lub sześciokątne (hexagonalne). Przy czym poszczególne parametry prognostyczne modelu mogą być zapisane na różniących się siatkach. Mamy tu do czynienia z różnymi typami siatki w klasyfikacji Arakawy, na których wszystkie zmienne równań mogą leżeć w tej samej lokalizacji (siatka A) lub parametry dynamiczne (składowe prędkości lub wirowości) i skalarne (temperatura, wilgotność, ciśnienie) mogą leżeć na siatkach przesuniętych względem siebie o połowę oczka siatki (siatki B, C, D ,E).
(17) Pionowa struktura siatki – w modelach NWP stosuje się zwykle siatki, w których wysokości poszczególnych poziomów obliczeniowych zmieniają się zgodnie ze zmianą wysokości powierzchni ziemi poniżej (ang. terrain-following coordinates). Może to dotyczyć całej domeny obliczeniowej lub tylko jej dolnej części (ang. hybrid coordinates). W tym ostatnim przypadku w górnej części domeny poziomy modelu mogą znajdować się na stałej wysokości nad poziomem morza (ang. height levels) lub na stałych poziomach ciśnieniowych (ang. pressure lub sigma levels).
(18) Rozdzielczość przestrzenna – oznacza zwykle poziomą odległość pomiędzy sąsiednimi węzłami sieci obliczeniowej. Węzły sieci są najczęściej od siebie równooddalone w kierunkach horyzontalnych, choć niektóre modele dopuszczają zmienne odległości, aby umożliwić gęstsze pokrycie interesującego obszaru. Zmiany odległości pomiędzy węzłami mogą być wprowadzane lokalnie w ramach jednej siatki obliczeniowej (ang. stretching) lub poprzez stosowanie dodatkowej lokalnej siatki o większej ilości punków (ang. nesting). W tym ostatnim przypadku wymiana informacji pomiędzy siatkami zachodzić może w jednym kierunku od siatki rzadszej do gęstszej (ang. one-way nesting) lub następuje dwukierunkowa komunikacja (ang. two-way nesting). Obecnie typowe poziome odległości pomiędzy węzłami w operacyjnych modelach globalnych wynoszą od 6 do kilkunastu km, a dla regionalnych modeli NWP od 1 do kilku kilometrów. Pionowe odległości pomiędzy sąsiednimi poziomami węzłów zmieniają się z wysokością, od kilkudziesięciu metrów przy powierzchni podłoża do kilkuset metrów w głębi atmosfery. Gęstość siatki numerycznej zależy od mocy obliczeniowej stosowanych superkomputerów. Im większa moc, tym więcej operacji można wykonać w ograniczonym czasie przeznaczonym na obliczenie prognozy, a więc tym więcej węzłów może zawierać sieć obliczeniowa modelu i tym mniejsza może być odległość pomiędzy nimi.
(19) Rozdzielczość modelu – w terminologii naukowej przez rozdzielczość modelu rozumieć można także przestrzenny rozmiar najmniejszego obiektu meteorologicznego, którego ewolucja może być poprawnie przedstawiona przez ten model. Rozmiar ten jest około 5 do 8 razy większy niż pozioma odległość pomiędzy sąsiednimi węzłami sieci obliczeniowej. Wiąże się to z możliwością poprawnego opisu struktury i ewolucji cyrkulacji (np. pola wirowego) odpowiedzialnych za rozwój obiektu. Dotyczy to na przykład rozwoju komórek konwekcyjnych powstających w warstwie granicznej atmosfery. W praktyce warto doprecyzować, które z dwu znaczeń rozdzielczości modelu stosowane jest w danym stwierdzeniu.
(20) Zakres i rozdzielczość czasowa prognoz – pojęcia określające zwykle długość prognozy (lub wyprzedzenie) od momentu jej startu oraz krok prognozy (czyli częstość zapisu jej wyników). Są to parametry dobierane w miarę dowolnie, ale także ograniczone mocą obliczeniową komputerów oraz wielkością dostępnych zasobów bazodanowych, na których przechowywane są i dalej przetwarzane wyniki prognoz. Należy także uwzględnić zakres stosowalności prognoz, ponieważ numeryczne błędy prognozy rosną z jej wyprzedzeniem i po okresie kilku dni zaczynają dominować w jej wynikach.
(21) Krok całkowania – parametr często mylony z krokiem prognozy. Określa on wewnętrzny krok czasowy wykorzystywany do wyliczenia kolejnych stanów atmosfery w procesie obliczania prognozy czyli całkowania równań numerycznych na siatce obliczeniowej. Wielkość kroku całkowania zależy od rozmiaru oczek siatki obliczeniowej. Jego wartość jest ograniczona warunkami stabilności zaimplementowanych algorytmów numerycznych. Stosowanie dłuższego kroku całkowania przyspiesza obliczenia, ponieważ wykonuje się ich mniej dla danego zakresu prognozy. W przypadku modeli globalnych krok całkowania wynosi kilka minut, dla modeli regionalnych o dużej rozdzielczości jego wartość się zmniejsza do kilkudziesięciu lub nawet kilkunastu sekund.
(22) Warunki stabilność modelu – zależą zwykle od wielkości kroku czasowego, rozdzielczości przestrzennej i lokalnej prognozowanej szybkości przepływu (prędkości wiatru). Są to warunki, które określają kiedy numeryczne przybliżenia równań ruchu pozostają stabilne i nie zachodzi w nich gwałtowny, niekontrolowany wzrost wielkości błędów, oznaczający, że wyniki prognozy przestają mieć sens fizyczny. Generalnie, warunki te oznaczają, że nie można dowolnie wydłużać kroku całkowania modelu. W przypadku modeli Eulerowskich (równania modelu uwzględniają tylko to, co dzieje się na poszczególnych węzłach siatki) musi on być na tyle mały, żeby w kolejnych krokach czasowych model dobrze kontrolował („widział”) przenoszenie informacji pomiędzy węzłami siatki poprzez sam prognozowany przepływ, a więc, żeby ta informacja nie była przenoszona na zbyt dalekie odległości. Wtedy krok całkowania Δt jest ograniczony przez tzw. warunek Couranta lub CFL (Courant-Friedrichs-Lewy): Δt < Δx/U (gdzie Δx to rozmiar oczka siatki obliczeniowej a U to prędkość przepływu). W przypadku modeli semi-Lagranżowskich (równania ruchu uwzględniają trajektorie cząstek, które w każdym kroku czasowym doprowadzają je do poszczególnych węzłów siatki obliczeniowej), stabilność schematu obliczeniowego zapewniona jest przez stabilność obliczania tych trajektorii w zmiennym przestrzennie polu prędkości i stosowne kryterium Lipschitza jest Δt*|dU/dx| < 1. Ponieważ kryterium to dopuszcza kilkukrotnie większy krok całkowania niż w przypadku warunku stabilności CFL, większość operacyjnych modeli NWP to modele semi-Lagranżowskie.
(23) Dokładność prognoz numerycznych – w praktyce amplituda i lokalizacja kluczowych parametrów zależy m.in. od gęstości siatki obliczeniowej, czyli od odległości pomiędzy jej sąsiednimi węzłami. Im mniejsza odległość, tym gęstsza sieć i lepsze przybliżenie. Przy czym zwykle poprawa jakości prognozy zależy także silnie od wielu dodatkowych czynników, takich jak dokładność wyznaczenia warunków brzegowych i początkowych, jakość pól stałych opisujących parametry podłoża, dokładność opisu zachodzących procesów fizycznych w postaci parametryzacji i algorytmów numerycznych.
(24) Parametryzacje – niektóre procesy fizyczne opisujące zmiany zachodzące w atmosferze są zbyt złożone, aby można je było poprawnie opisać w skalach rozpoznawanych przez model. Modele NWP uwzględniają związki oraz obliczają przybliżone efekty takich procesów za pomocą specjalnych procedur zwanych parametryzacjami. Typowe parametryzacje wykorzystywane przez modele NWP dotyczą procesów zachodzących w glebie, wymiany pędu oraz strumieni ciepła i wilgotności pomiędzy atmosferą i podłożem, płytkiej i głębokiej konwekcja termiczna, procesów mikrofizycznych i radiacyjnych oraz turbulencji.
(25) Procesy podskalowe – modele NWP muszą uwzględnić także fakt, że poszczególne procesy atmosferyczne odbywają się w obszarach o różnych wielkościach. Niektóre procesy mają miejsce w tak małych objętościach atmosfery, że nie mogą być bezpośrednio odwzorowane na siatce obliczeniowej modelu. Dotyczy to w szczególności procesów radiacyjnych, turbulencyjnych lub procesów mikrofizyki chmurowej związanych z kondensacją pary wodnej oraz tworzeniem chmur i opadów, które odbywają się w skalach centymetrowych, a nawet mniejszych.
(26) Warunki początkowe (IC) i brzegowe (BC) – procedury modelu mogą rozpocząć obliczanie prognozy pod warunkiem dostarczenia im informacji o stanie atmosfery w momencie, który jest początkiem okresu prognostycznego. Informacja ta (tzw. warunki początkowe) musi być zadana we wszystkich węzłach 3-wymiarowej sieci obliczeniowej, a dla wiarygodnej prognozy powinna być jak najbliższa rzeczywistemu stanowi atmosfery w tym momencie. W przypadku modeli globalnych warunki początkowe są konstruowane w procesie asymilacji danych dostępnych z globalnych sieci pomiarowych (stacje telemetryczne, statki, boje, samoloty, balony, satelity). Wyniki modeli globalnych wykorzystywane są natomiast jako warunki początkowe i brzegowe w modelach prognoz regionalnych. Dodatkowo, modele regionalne mogą także stosować procedury asymilacji dodatkowych dostępnych danych obserwacyjnych, tak aby zwiększyć reprezentatywność i dokładność swoich danych początkowych.
(27) Proces asymilacji danych – wymagane wartości początkowe (IC) poszczególnych parametrów meteorologicznych obliczane są przez specjalne procedury na podstawie wyników bieżących obserwacji i pomiarów meteorologicznych (przyziemnych, balonowych, satelitarnych, etc.) oraz wyników prognoz (zwykle kilkugodzinnych) samego modelu. W procesie asymilacji danych następuje redukcja błędów modelu poprzez dopasowanie stanu atmosfery na siatce numerycznej do znanych wartości pomiarowych w rzeczywistych lokalizacjach. Do najczęściej stosowanych metod asymilacji należą nudging (lokalne dopasowywanie rozwiązań modelu w bliskiej, z góry przyjętej odległości przestrzennej i czasowej do znanego pomiaru) oraz statystyczne metody wariacyjne (stosowane dla 3-wymiarowej przestrzeni fizycznej 3DVAR oraz stosowane dla tej przestrzeni i pewnego interwału czasowego 4DVAR), a także wykorzystujące filtry Kalmana lub kombinację tych ostatnich z metodami wariacyjnymi. Metody statystyczne polegają na globalnej iteracyjnej minimalizacji błędu przez dopasowywanie zbalansowanego stanu całej atmosfery do istniejących obserwacji. W praktyce metody nudgingu powodują lepszą poprawę rozwiązań w obszarach bliższych stacjom pomiarowym, w krótszym okresie czasu. Metody wariacyjne zdobywają przewagę przy dłuższych prognozach i w obszarach gdzie jest mniejsza ilość informacji pomiarowej.
(28) Standardowe wyniki prognoz – zwykle różne formy graficzne ukazujące przestrzenny rozkład wybranych parametrów meteorologicznych w określonych chwilach prognozy:
- mapy rozkładu parametrów meteorologicznych przy powierzchni ziemi lub w górnej atmosferze, np. na powierzchniach stałego ciśnienia (izobarycznych) lub na stałych wysokościach nad powierzchnią gruntu lub poziomem morza;
- przekroje pionowe;
- sondaże aerologiczne nad wybraną lokalizacją.
Ponadto wytwarzane są meteogramy przedstawiające prognozowaną ewolucję wybranych parametrów meteorologicznych dla określonej lokalizacji (np. wybranej miejscowości).
(29) Specjalista modelowania pogody – rozwój i utrzymanie systemów operacyjnego modelowania pogody wymaga wiedzy i umiejętności w wielu dziedzinach, a zatem sformułowanie to obejmuje zarówno badaczy zajmujących się rozwojem teoretycznych podstaw modelowania, jak i ekspertów odpowiedzialnych za wdrażanie nowych rozwiązań, utrzymywanie i monitoring poprawności działania systemu prognostycznego oraz przygotowywanie produktów dla końcowych użytkowników. Odpowiednie dziedziny wiedzy obejmują metody numeryczne, metody statystyczne, programowanie i informatykę, asymilację danych obserwacyjnych, dynamikę i fizykę procesów w atmosferze i podłożu, weryfikację i interpretację wyników.
Bauer P., Thorpe A., Brunet G., 2015, The quiet revolution of numerical weather prediction, Nature, 525 (7567), 47-55, DOI: 10.1038/nature14956.
Fletcher C.A.J., Computational Techniques for Fluid Dynamics, Vol. 1, Springer, 401 s.
Fletcher C.A.J., Computational Techniques for Fluid Dynamics, Vol. 2, Springer, 494 s.
Haltiner G.J., Williams R.T., 1983, Numerical Prediction and Dynamic Meteorology, Wiley and Sons Ltd., 477 s.
Kalnay E., 2002, Atmospheric Modeling, Data Assimilation and Predictability, Cambridge University Press, 368 s.
Krishnamurti T.N., Bounoua L., 1995, An Introduction to Numerical Weather Prediction Techniques, CRC Press, 293 s.
Łobocki L., 2018, Podstawy dynamiki atmosfery, Oficyna Wydawnicza Politechniki Warszawskiej, Warszawa, 550 s.
Michaelides S. (red.), 2021, Precipitation Science. Measurement, Remote Sensing, Microphysics and Modeling, Elsevier, 870 s.
Navon I.M., 2009, Data assimilation for numerical weather prediction: A review, [w:] Data Assimilation for Atmospheric, Oceanic and Hydrologic Applications, S.K. Park, L. Xu (red.), Springer, 21-65, DOI: 10.1007/978-3-540-71056-1_2.
Ólafsson H., Bao J.-W. (red.), 2021, Uncertainties in Numerical Weather Prediction, Elsevier, DOI: 10.1016/C2017-0-03301-3.
Pielke R.A., 2002, Mesoscale Meteorological Modeling, Academic Press, 696 s.
Prosnak W.J., 1993, Wprowadzenie do numerycznej mechaniki płynów. Część A. Podstawowe metody numeryczne, Maszyny Przepływowe, tom 12, Wydawnictwo Ossolineum, 490 s.
Warner T.T., 2010, Numerical Weather and Climate Prediction, Cambridge University Press, DOI: 10.1017/CBO9780511763243.
Wilks D.S., 2006, Statistical Methods in the Atmospheric Sciences, Academic Press, 649 s.
Yano J.-I., Ziemiański M.Z., Cullen M., Termonia P., Onvlee J., Bengtsson L., Carrassi A., Davy R., Deluca A., Gray S.L., Homar V., Köhler M., Krichak S., Michaelides S., Phillips V.T.J., Soares P.M.M., Wyszogrodzki A.A., 2018, Scientific challenges of convective-scale numerical weather prediction, Bulletin of the American Meteorological Society, 99 (4), 699-710, DOI: 10.1175/BAMS-D-17-0125.1.
dokładność prognoz numerycznych (23)
domena obliczeniowa (15)
generalna charakterystyka numerycznych modeli pogody (XIV)
konsorcja numerycznego modelowania pogody (1)
krok całkowania (21)
metody numeryczne (14)
model ALARO (ALADIN and AROME) (2)
model AROME (3)
model burzowy TSP (4)
model COSMO (5)
model ECMWF EPS 46 (7)
model estymacji pola opadu (RainGRS) (6)
model INCA-PL2 (8)
model opadu MERGE (9)
model WRF GFS MEDIUM (12)
model WRFICON (11)
model WRF METEOPG (10)
norma (prognozy długoterminowe) (VIII)
numeryczne modele pogody (XII)
numeryczne modele prognoz pogody (NWP) (13)
parametryzacje (24)
pionowa struktura siatki (17)
proces asymilacji danych (27)
procesy podskalowe (25)
prognoza długoterminowa (II)
prognoza długoterminowa – szczegółowa (III)
prognoza długoterminowa – tygodniowa (IV)
prognoza długoterminowa – dekadowa (V)
prognoza długoterminowa – miesięczna (VI)
prognoza długoterminowa – sezonowa (VII)
prognoza nowcastingowa (IX)
prognoza numeryczna (XI)
prognoza ogólnego charakteru modelu (I)
prognoza ultra-krótkoterminowa (X)
rozdzielczość modelu (19)
rozdzielczość numerycznych modeli pogody (XIII)
rozdzielczość przestrzenna (18)
specjalista modelowania pogody (29)
standardowe wyniki prognoz (28)
struktura siatki obliczeniowej (16)
warunki początkowe (IC) i brzegowe (BC) (26)
warunki stabilność modelu (22)

