Wykrywanie ekstremalnych wartości parametrów meteorologicznych w prognozach wiązkowych ECMWF za pomocą parametrów EFI i SOT
Opracowanie:
dr Michał Ziemiański, Zakład Prognoz Numerycznych COSMO
dr inż. Marta Gruszczyńska, Zakład Analiz Meteorologicznych i Prognoz Długoterminowych
Robert Przyłuski, Zakład Analiz Meteorologicznych i Prognoz Długoterminowych
a. Prezentacja prognoz zjawisk ekstremalnych
Prognozy zjawisk ekstremalnych ECMWF udostępniane są jako prognozy średnioterminowe z rozdzielczością przestrzenną 0.2° x 0.2° na 7-10 dni oraz prognozy długoterminowe z rozdzielczością przestrzenną 0.4° x 0.4° jako prognozy tygodniowe na 6 tygodni. Na stronie Centrum Modelowania Meteorologicznego prezentujemy EFI (ang. Extreme Forecast Index) oraz SOT (ang. Shift of Tails) dla dziesięciu parametrów meteorologicznych przedstawionych w tabeli. SOT prezentowany jest na mapach za pomocą czarnych izolinii od 0 co 0.5 i dodatkowo zastosowano linię przerywaną dla 0.2.
|
Rozdzielczość czasowa |
Czas wyprzedzenia |
Aktualizacja |
Parametry |
|
|
Prognozy średnioterminowe Rozdzielczość przestrzenna: 0.2° x 0.2° lat/long |
||||
|
Prognoza na 1 dzień |
7 dni |
Codziennie |
suma dobowa |
|
|
średnia |
|
|||
|
Oznaczenie na stronie jako 1 dzień (7 dni) |
||||
|
ekstrema |
|
|||
|
Prognoza na 3 dni |
9 dni |
Codziennie |
suma dobowa |
|
|
Oznaczenie na stronie jako 3 dni (9 dni) |
średnia |
|
||
|
Prognoza na 5 dni |
9 dni |
Codziennie |
suma dobowa |
|
|
Oznaczenie na stronie jako 5 dni (9 dni) |
średnia |
|
||
|
Prognoza na 10 dni |
10 dni |
Codziennie |
suma dobowa |
|
|
Oznaczenie na stronie jako 10 dni |
średnia |
|
||
|
Prognozy długoterminowe Rozdzielczość przestrzenna: 0.4° x 0.4° lat/long |
||||
|
Prognoza na 1 tydzień |
6 tygodni |
Dwa razy w tygodniu (wtorek, piątek) |
suma dobowa |
|
|
średnia |
|
|||
|
Oznaczenie na stronie jako tydzień (6 tygodni) |
||||
b. Interpretacja i analiza EFI i SOT: uwagi ogólne
Wskaźniki EFI i SOT mają umożliwić automatyczne wykrywanie w prognozach ECMWF możliwości wystąpienia ekstremalnej pogody. Mają one z definicji abstrakcyjną strukturę i działają poprzez porównanie probabilistycznej prognozy wiązkowej z klimatem modelu. Wskaźniki te są tak skalowane, aby mogły być stosowane dla dowolnych parametrów meteorologicznych, a ich wartości nie są czułe na lokalną zmienność klimatu wartości ekstremalnych (działają tak samo dla obszarów o mniejszych lub większych ekstremach pogodowych). Wynika z tego jednak, że trudno bezpośrednio interpretować je ilościowo w znaczeniu konkretnych wielkości prognozowanych parametrów meteorologicznych. Dają one raczej informację probabilistyczną o prawdopodobieństwie wystąpienia bardzo dużych lub ekstremalnych wielkości parametrów meteorologicznych (EFI), a rosnące wartości (bezwzględne) wskaźnika SOT wskazują zarówno na rosnące prawdopodobieństwo wystąpienia wielkości ekstremalnych, jak i rosnącą wielkość przekroczenia przez wartość prognozowaną wielkości charakteryzujących ekstremum klimatu modelu.
Zatem główną intencją zawartą w definicji tych wskaźników jest sygnalizacja istotnej możliwości (w znaczeniu probabilistycznym) wystąpienia ekstremalnych wielkości pogodowych z jak największym wyprzedzeniem czasowym, a w mniejszym stopniu prognozę ich bezwzględnej wartości. Ta ostatnia powinna wykorzystywać dodatkowo dokładną całościową analizę sytuacji meteorologicznej. Informacja oparta na prognostycznych wartościach EFI i SOT ma jednak istotne znaczenie, ponieważ pozwala na wcześniejsze uprzedzanie (na przykład instytucji odpowiedzialnych za bezpieczeństwo publiczne), że istnieje możliwość wystąpienia sytuacji o bardzo dużych lub ekstremalnie wysokich wielkościach parametrów meteorologicznych, a także zwrócenie uwagi na sytuacje, których dokładniejsza analiza jest szczególnie potrzebna.
W praktycznej interpretacji relacje pomiędzy prognozą, a klimatem modelu (reprezentowane przez EFI i SOT) będą przenoszone na relacje pomiędzy prognozą, a rzeczywiście zaobserwowanymi bardzo dużymi i ekstremalnymi wielkościami danego parametru w interesującym obszarze i porze roku, czyli rzeczywistym klimatem wartości ekstremalnych. Wskaźniki te przeznaczone są zatem dla profesjonalnego odbiorcy, który powinien dobrze rozumieć ich probabilistyczny charakter oraz mieć obycie z podstawową charakterystyką prognoz numerycznych i ich interpretacją. Interpretacja tych wskaźników wymaga też bardzo dobrej znajomości rzeczywistego klimatu wartości ekstremalnych analizowanych parametrów meteorologicznych, w tym jego zmienności przestrzennej oraz sezonowej.
Praktyczne stosowanie tych wskaźników wymaga także wcześniejszych analiz i zebrania doświadczeń wskazujących jak w rzeczywistych sytuacjach pogodowych prognozowane rozkłady EFI i SOT odnoszą się do rzeczywiście obserwowanych wielkości meteorologicznych. I tak, z informacji opublikowanych dla EFI wynika generalnie (Zsoter 2006), że poszczególne wartości tego wskaźnika oznaczają:
- wartości bezwzględne w przedziale od 0.50 do 0.80 (niezależnie od znaku) oznaczają rzadką/nietypową (ang. unusual) pogodę,
- wartość bezwzględne przekraczające 0.80 (niezależnie od znaku) oznaczają bardzo rzadką/bardzo nietypową (ang. very unusual) lub ekstremalną pogodę,
- EFI = +1 występuje, gdy prognozowane wartości wszystkich elementów wiązki są powyżej ekstremum (maksimum) klimatu modelu. W przypadku temperatury powietrza oznacza to, że spodziewane są bardzo wysokie temperatury w stosunku do rzeczywistego klimatu,
- EFI = -1 występuje, gdy prognozowane wartości wszystkich realizacji wiązki są poniżej ekstremum (minimum) klimatu modelu. W przypadku temperatury powietrza oznacza to, że spodziewane są bardzo niskie temperatury w stosunku do rzeczywistego modelu.
Należy się przy tym spodziewać, że statystyczne charakterystyki klimatu wartości ekstremalnych mogą być różne dla różnych parametrów meteorologicznych. Zatem praktyczna interpretacja konkretnych rozkładów tych wskaźników, w tym zwłaszcza SOT, może w istotny sposób zależeć od rodzaju parametru meteorologicznego, którego dotyczy.
Ze względu na konstrukcję wskaźników, nakierowaną na sygnalizowanie możliwości ekstremalnej pogody (porównywalnej lub przekraczającej klimat modelu) wtedy, kiedy prawdopodobieństwo jej wystąpienia uważane jest za znaczące, ale nie koniecznie bardzo wysokie (dla SOT już w granicach 10%), można spodziewać się pewnej ilości nietrafnych prognoz wskazujących na możliwość wystąpienia takiej pogody. Jest to sytuacja tzw. fałszywych alarmów i jest sygnalizowana także w literaturze (Boisserie 2016). Także ten aspekt powinien być brany pod uwagę podczas analizy tych wskaźników. Jest to dodatkowy argument za koniecznością zebrania praktycznych doświadczeń w ich interpretacji oraz za faktem, że są one przeznaczone dla profesjonalnego odbiorcy.
Należy też spodziewać się sytuacji odwrotnych, kiedy wskaźniki EFI i SOT nie będą wskazywać na możliwość wystąpienia zjawisk ekstremalnych, które w rzeczywistości wystąpią. Może to dotyczyć przede wszystkim zjawisk o stosunkowo małej skali przestrzennej (np. konwekcyjnych), które jeszcze nie są odpowiednio reprezentowane przez współczesne model globalne, jak model IFS ECMWF, ze względu na ich niewystarczającą rozdzielczość przestrzenną. Aby w pewien sposób uwzględnić także i tego typu niebezpieczne zjawiska, ECMWF rutynowo oblicza wartości EFI i SOT dla wybranych wskaźników konwekcyjnych, które nie tyle odnoszą się do obserwowanej ekstremalnej pogody, ile do prognozowanego w atmosferze potencjału do powstawania groźnych zjawisk konwekcyjnych, generujących taką pogodę.
Należy też zwrócić uwagę, że ze względu na nieuniknione błędy modeli, obszary dużych wartości wskaźników EFI i SOT mogą być przestrzennie przesunięte w stosunku do obszarów rzeczywistej ekstremalnej pogody, zwłaszcza dla wielodniowego wyprzedzenia prognozy. Zatem praktyczna analiza tych wskaźników powinna brać pod uwagę obszar większy niż bezpośrednio osłaniany.
EFI i SOT obliczane są rutynowo w ECMWF dla wielu istotnych parametrów meteorologicznych charakteryzujących ekstremalną pogodę. Dotyczy bezpośrednio obserwowanych wielkości, takich jak temperatury ekstremalne, porywy wiatru i opady. Dotyczy to też wielkości, które nie są bezpośrednio obserwowane, ale opisują stan atmosfery, w którym istnieje duży potencjał do powstawania ekstremalnej pogody. Tego typu parametry obejmują wybrane wskaźniki konwekcyjne: CAPE (Convectively Available Potential Energy, opisujący wielkość energii dostępnej dla procesów konwekcyjnych) oraz CAPE-SHEAR Parameter (CSP, łączący CAPE z informacją o zmienności wiatru z wysokością i odnoszący się do możliwości powstawania szczególnie niebezpiecznych systemów zorganizowanej konwekcji); porównaj dyskusję w Tsonevsky (2015) oraz przykłady w Magnusson i inni (2017) dla szczególnie groźnego derecho nad Polską z 11 sierpnia 2017. Dla wielkoskalowych procesów odpowiedzialnych za silne opady jest to atmosferyczny strumień pary wodnej odzwierciedlający obecność tzw. „rzek atmosferycznych” transportujących duże ilości pary wodnej i umożliwiających długotrwałe i obfite opady na stosunkowo dużych obszarach; porównaj dyskusję w Cox i Lavers (2020).
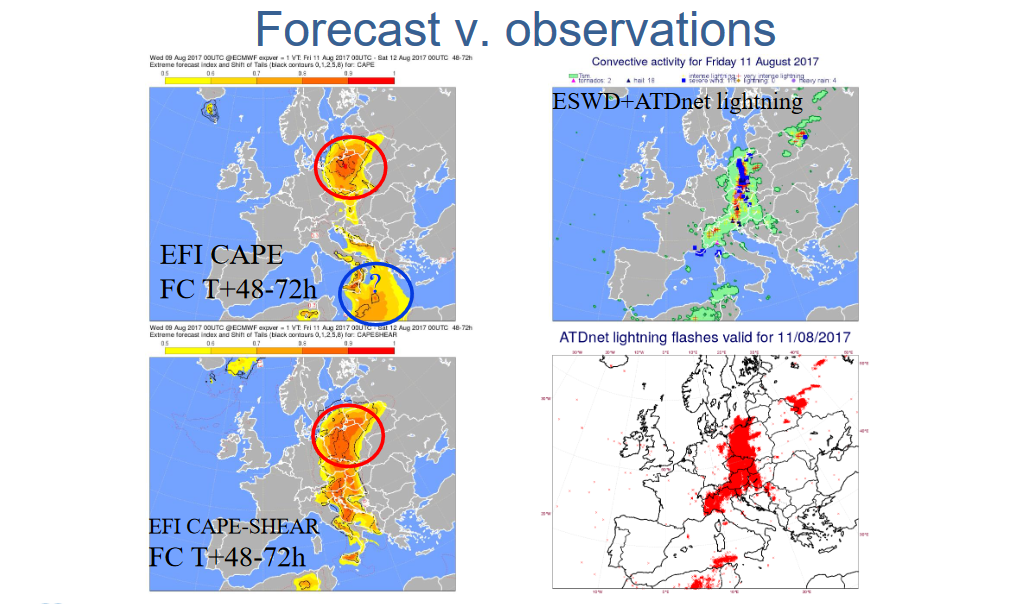 Rys. 1. Prognoza EFI CASE i CAPE-SHEAR (po lewej) wraz z liczbą zarejestrowanych wyładowań (po prawej) (Tsonevsky (2018)). Prognozowano EFI dla parametrów: indeks chwiejności atmosfery (CAPE) oraz indeks chwiejności atmosfery i ścinania wiatru (CAPES) od 0.5 do 1.
Rys. 1. Prognoza EFI CASE i CAPE-SHEAR (po lewej) wraz z liczbą zarejestrowanych wyładowań (po prawej) (Tsonevsky (2018)). Prognozowano EFI dla parametrów: indeks chwiejności atmosfery (CAPE) oraz indeks chwiejności atmosfery i ścinania wiatru (CAPES) od 0.5 do 1.
c. Przykłady wizualizacji na stronie IMGW-PIB CMM
Opad całkowity
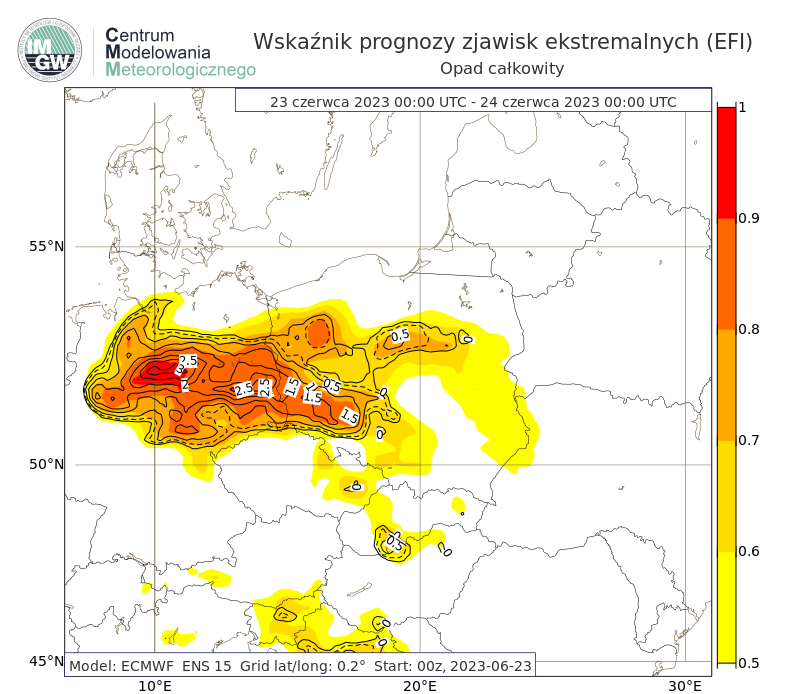
Rys. 2. Przykład prognozy wskaźnika prognozy zjawisk ekstremalnych dla opadu atmosferycznego na 23 czerwca 2023 r. Na terenie Polski prognozowane są wyższe opady niż wartości klimatu modelu, wartość wskaźnika wskazuje na rzadką/nietypową (ang. unusual) pogodę (EFI od 0.50 do 0.80), a także w zachodniej Polsce bardzo rzadką/bardzo nietypową (ang. very unusual) lub ekstremalną pogodę (EFI powyżej 0.80). Wartość SOT wynosi od 0 do 2.5. Już wartości SOT powyżej 0 wskazują na istotną możliwość przekroczenia przez prognozę wartości ekstremalnych klimatu modelu, a wielkości istotnie większe wskazują, że takie przekroczenia oraz prawdopodobieństwo ich wystąpienia są wysokie.
Temperatura powietrza 2m
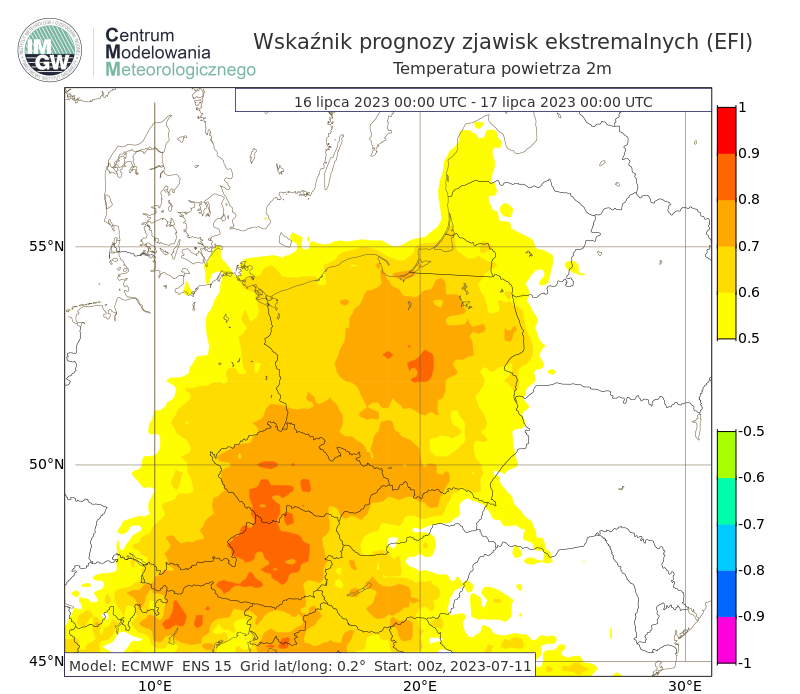
Rys. 3. Przykład prognozy wskaźnika prognozy zjawisk ekstremalnych dla temperatury powietrza z 11 lipca 2023 roku na 16 lipca 2023 r. Na terenie Polski prognozowane są wyższe temperatury powietrza niż wartości klimatu modelu, wartość wskaźnika wskazuje na rzadką/nietypową (ang. unusual) pogodę (EFI od 0.50 do 0.80), a także w centralnej Polsce bardzo rzadką/bardzo nietypową (ang. very unusual) lub ekstremalną pogodę.
Maksymalna temperatura powietrza 2m
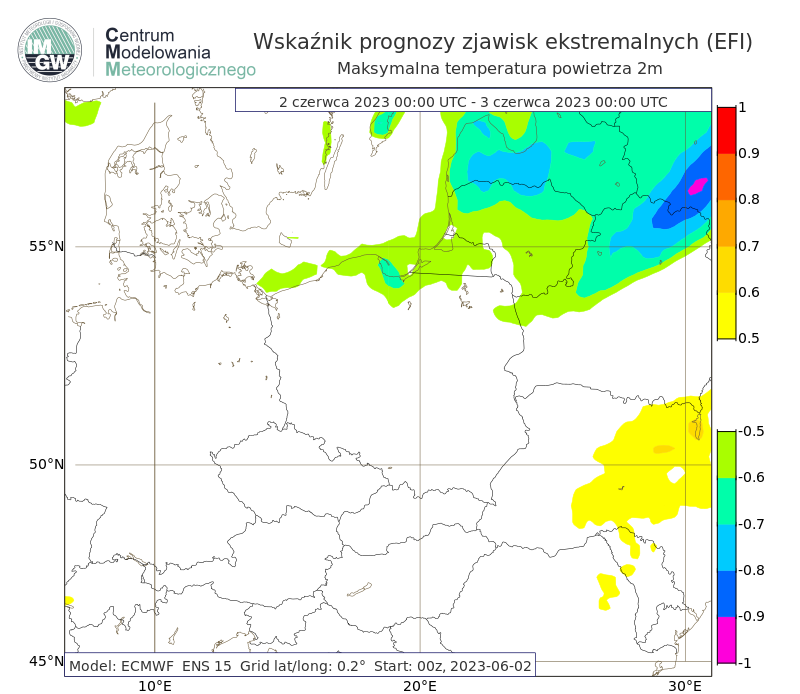
Rys. 4. Przykład prognozy wskaźnika prognozy zjawisk ekstremalnych dla maksymalnej temperatury powietrza z 2 czerwca 2023 roku na 2 czerwca. Na terenie północnej Polski prognozowane były niższe maksymalne temperatury powietrza niż wartości klimatu modelu. Wartość wskaźnika wskazuje na rzadką/nietypową (ang. unusual) pogodę (EFI od -0.70 do -0.50). 2 czerwca 2023 roku zanotowano na stacjach synoptycznych najniższą maksymalną temperaturę powietrza dla czerwca m.in. dla stacji Gdańsk (14°C), Koszalin (14°C), Olsztyn (16°C).
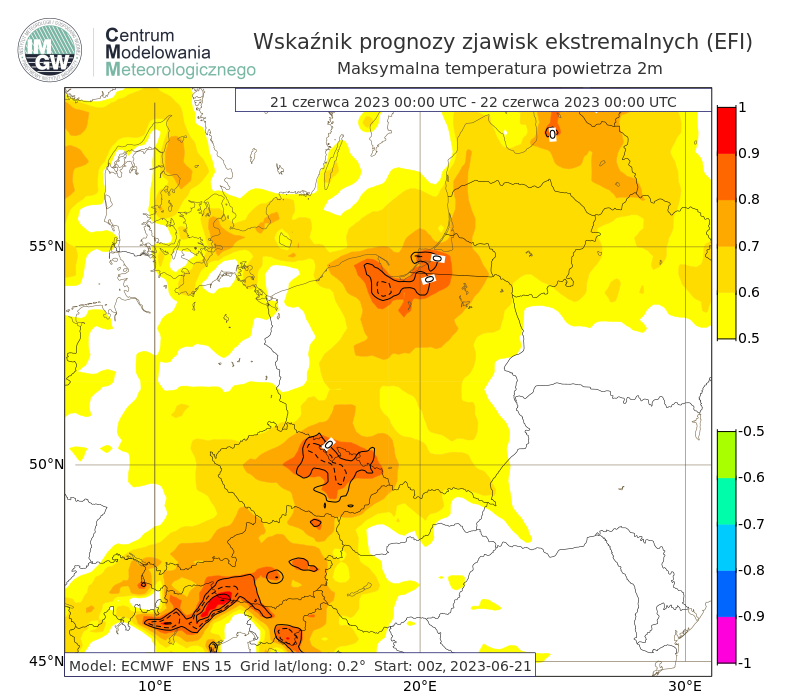
Rys. 5. Przykład prognozy wskaźnika prognozy zjawisk ekstremalnych dla maksymalnej temperatury powietrza z 21 czerwca 2023 roku na 21 czerwca. Na terenie Polski prognozowane są wyższe maksymalne temperatury powietrza niż wartości klimatu modelu. Wartość wskaźnika wskazuje na rzadką/nietypową (ang. unusual) pogodę (EFI od 0.50 do 0.80), a także na północy bardzo rzadką/bardzo nietypową (ang. very unusual) lub ekstremalną pogodę (EFI poniżej 0.80). 21 czerwca na stacjach synoptycznych zanotowano najwyższą w miesiącu temperaturę maksymalna m.in. dla stacji Gdańsk (30°C), Olsztyn (31°C). Wartość SOT wynosi od 0 do 0.2, co już wskazuje na istotną możliwość przekroczenia przez prognozę wartości ekstremalnych klimatu modelu.
Minimalna temperatura powietrza 2m
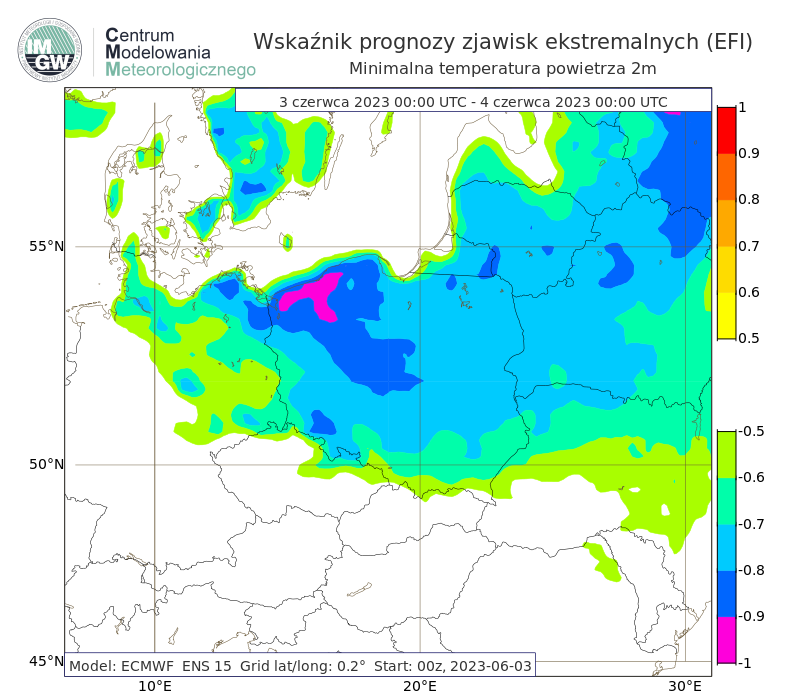
Rys. 6. Przykład prognozy wskaźnika prognozy zjawisk ekstremalnych dla minimalnej temperatury powietrza z 3 czerwca 2023 roku na 3 czerwca. Na terenie Polski prognozowane są niższe minimalne temperatury powietrza niż wartości klimatu modelu. Wartość wskaźnika wskazuje na rzadką/nietypową (ang. unusual) pogodę (EFI od -0.80 do -0.50), a także w północno-wschodniej Polsce bardzo rzadką/bardzo nietypową (ang. very unusual) lub ekstremalną pogodę (EFI poniżej -0.80). 3 czerwca 2023 roku zanotowano na stacjach synoptycznych w m.in. Szczecinie (1°C), Koszalinie (3°), Olsztynie (2°), Toruniu (2°) najniższą minimalną temperaturę powietrza dla czerwca w 2023 roku.
Porywy wiatru 10m
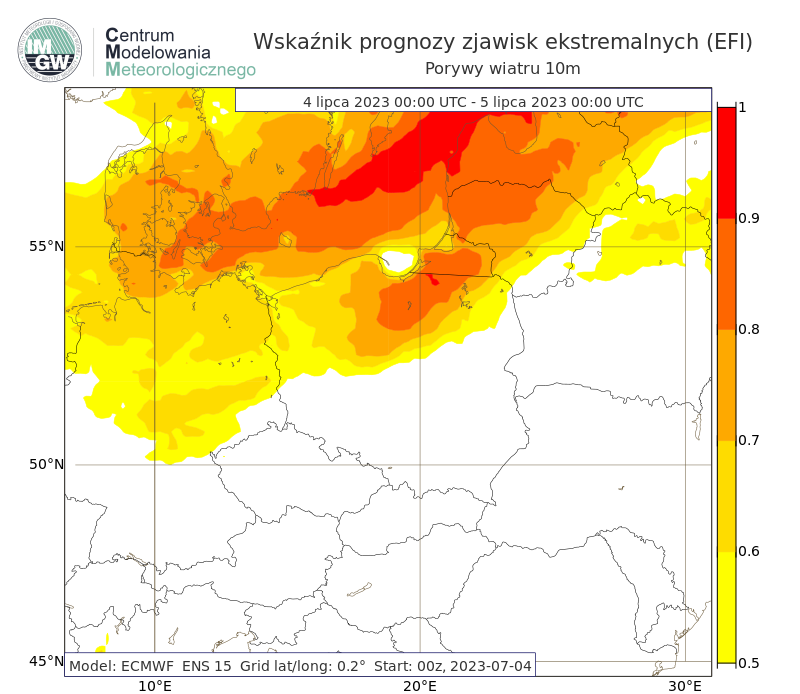
Rys. 7. Przykład prognozy wskaźnika prognozy zjawisk ekstremalnych dla porywu wiatru na 10 m z 4 lipca 2023 roku. Na terenie Morza Bałtyckiego prognozowane są wartości EFI powyżej 0.9. Na terenie północnej Polski rzadką/nietypową (ang. unusual) pogodę (EFI od 0.50 do 0.80), a także bardzo rzadką/bardzo nietypową (ang. very unusual) lub ekstremalną pogodę ekstremalną (wartość przekraczająca 0.80). W Ustce oraz Łebie zanotowano maksymalne porywy wiatru 61 km/h, w Kołobrzegu 83 km/h, w Toruniu 50 km/h, w Elblągu 58 km/h.
Prędkość wiatru 10 m
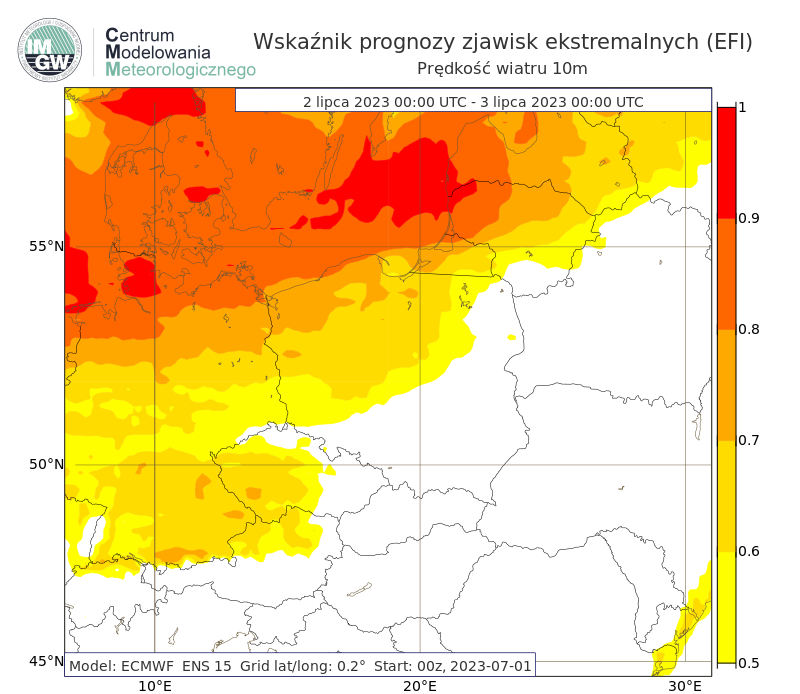
Rys. 8. Przykład prognozy wskaźnika prognozy zjawisk ekstremalnych dla prędkości wiatru na 10 m z 1 lipca 2023 roku na 2 lipca. Na terenie Morza Bałtyckiego prognozowane są wartości EFI powyżej 0.9. Na terenie północnej Polski prognozowano rzadką/nietypową (ang. unusual) pogodę (EFI od 0.50 do 0.80)
Indeks chwiejności atmosfery
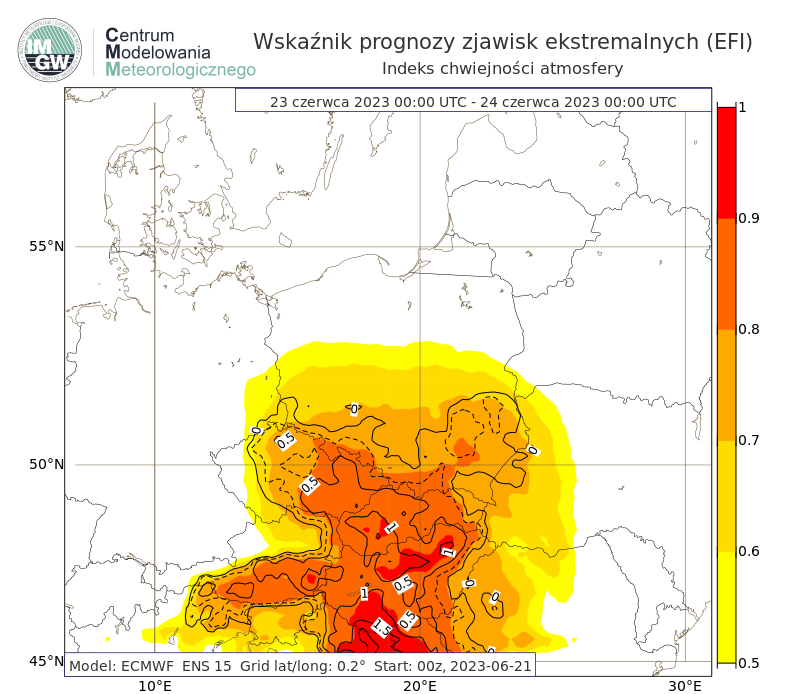
Rys. 9. Przykład prognozy wskaźnika prognozy zjawisk ekstremalnych dla indeksu chwiejności atmosfery, który opisuje wielkość energii dostępnej dla procesów konwekcyjnych z 21 czerwca 2023 roku na 23 czerwca. W południowej części Polski prognozowane były wartości EFI powyżej 0.8 co oznacza bardzo rzadką/bardzo nietypową (ang. very unusual) lub ekstremalną pogodę ekstremalną. Wartość SOT wynosi od 0 do 1. Już wartości SOT powyżej 0 wskazują na istotną możliwość przekroczenia przez prognozę wartości ekstremalnych klimatu modelu, a wielkości istotnie większe wskazują, że takie przekroczenia oraz prawdopodobieństwo ich wystąpienia są wysokie.
Indeks chwiejności atmosfery i ścinania wiatru
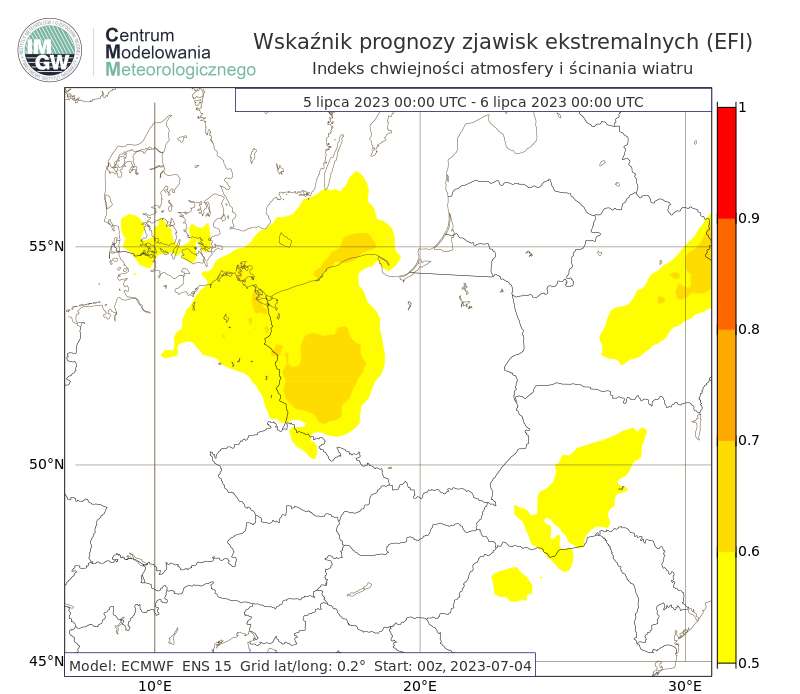
Rys. 10. Przykład prognozy wskaźnika prognozy zjawisk ekstremalnych dla indeksu chwiejności atmosfery i ścinania wiatru (wskaźnik konwekcyjny łączący CAPE z informacją o zmienności wiatru z wysokością i odnoszący się do możliwości powstawania szczególnie niebezpiecznych systemów zorganizowanej konwekcji) z 4 lipca 2023 roku na 5 lipca. We wschodniej Polsce prognozowane były wartości EFI od 0.5 do 0.7 co wskazywało na rzadką/nietypową (ang. unusual) pogodę.
Atmosferyczny strumień pary wodnej
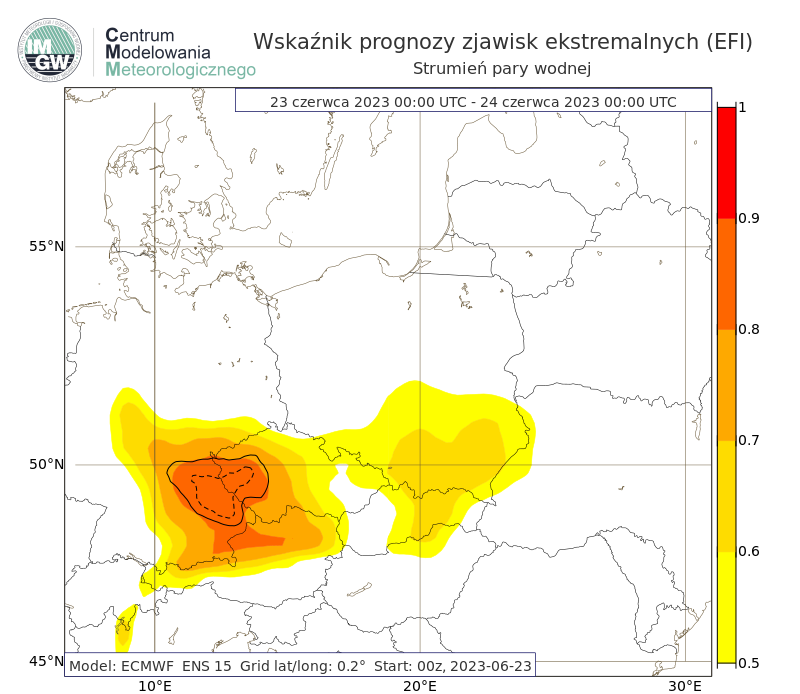
Rys. 11. Przykład prognozy wskaźnika prognozy zjawisk ekstremalnych dla atmosferycznego strumienia pary wodnej z 23 czerwca 2023 roku na 23 czerwca. W południowej Polsce prognozowane były wartości od 0.5 do 0.7 co wskazywało na rzadką/nietypową (ang. unusual) pogodę. Strumień pary wodnej odzwierciedla obecność tzw. „rzek atmosferycznych” transportujących duże ilości pary wodnej i umożliwiających długotrwałe i obfite opady na stosunkowo dużych obszarach. 23 czerwca zanotowano dla stacji synoptycznej w Zakopanem 42 mm opadu, w Rzeszowie 11 mm, w Opolu 28 mm, co stanowiło najwyższe wartości opadu w miesiącu.
d. Statystyczne definicje EFI i SOT
Dla dowolnego parametru/elementu meteorologicznego możemy, na podstawie jego dotychczasowych obserwacji, określić z jaką częstością obserwuje się występowanie różnych wartości tego parametru/elementu. Np. dla temperatury powietrza stosunkowo często występują umiarkowane jej wartości (powiedzmy około 10°C), a stosunkowo rzadko bardzo duże jej wartości (powiedzmy powyżej 30°C). Częstość, z jaką mierzone są różne wartości temperatury możemy przedstawić na wykresie, zwanym też histogramem, gdzie temperatura jest x-em, a jej częstość y-kiem. Jeśli mamy do dyspozycji wyniki prognozy wiązkowej, która w ECMWF zawiera 50 różnych realizacji dla prognozy na 15 dni i 100 różnych realizacji dla prognozy na 46 dni, to dla wybranego czasu i miejsca prognozy możemy także obliczyć częstość wystąpienia w prognozie poszczególnych wartości interesującego parametru meteorologicznego (np. temperatury). Częstość tę z reguły interpretujemy jako prawdopodobieństwo wystąpienia różnych wartości tego parametru w przyszłości.
Znając częstość występowania możliwych wartości jakiegoś parametru możemy określić, jak często przyjmował on wielkości mniejsze lub równe tej wartości. Np. możemy sprawdzić, jak często występowała temperatura mniejsza lub równa 10°C. Funkcja równa częstości występowania wielkości parametru nie większych od danej wartości jest nazywana dystrybuantą. Np. dystrybuanta dla temperatury pokazuje dla zmieniających się (rosnących) temperatur (które są na wykresie x-em) jak często występowały temperatury o wielkości mniejszej lub równej temu x-owi (częstości te są na wykresie y-kiem). Dystrybuanta jest funkcją rosnącą o wartościach zmieniających się od 0 do 1, ponieważ częstość występowania wartości parametru mniejszej od minimalnej wynosi 0, a częstość wystąpienia wartości mniejszej lub równej maksymalnej (czyli każdej z możliwych) wynosi 1.
Dystrybuanta okazuje się funkcją wygodną do prowadzenia analiz statystycznych. Pozwala ona na określanie istotnych cech charakteryzujących rozkład możliwych wartości danego parametru, w tym jego wartości przeciętnych i ekstremalnych. Służą do tego kwantyle, które są rodzajem działania odwrotnego na dystrybuancie. Mianowicie, dla danej wartości dystrybuanty, np. równej 0.5, kwantyl 0.5 jest tą wartością parametru meteorologicznego, dla której częstość występowania wartości mniejszych lub równych tej wartości wynosi 0.5. Podobnie zdefiniowane są kwantyle dla innych częstości występowania, np. 0.1, 0.25, 0.9, etc. Ogólnie, kwantyl odpowiadający częstości p dystrybuanty, czyli kwantyl p, jest tą wartością badanego parametru (np. temperatury), dla której częstość występowania wartości mniejszych lub równych tej wartości jest równa p.
Jeżeli znamy kwantyl p jakiegoś parametru, to wiemy, że wartości parametru mniejsze lub równe temu kwantylowi występują z częstością p, a wartości większe od niego z częstością 1- p, ponieważ wszystkie częstości sumują się do 1 (lub, jeśli ktoś woli, do 100%). Kwantyl 0.5 jest szczególny i jest nazywany medianą. Oznacza on taką wartość parametru (np. temperatury), dla której częstość występowania wartości nie większych od mediany wynosi 50%, i taka sama jest też częstość występowania wartości wyższych od mediany. Medianę można więc traktować jako wygodną miarę przeciętnej wartości danego parametru.
Kwantyle dla niskich i wysokich częstości występowania danego parametru używane są do charakteryzowania małych i dużych wartości tego parametru. Np. kwantyl 0.1 oznacza taką wartość parametru, dla której tylko w 10% obserwacji wystąpiły wielkości mniejsze lub równe wartości tego kwantyla. I tak, jeśli kwantyl 0.1 dla wszystkich zaobserwowanych temperatur wynosi na przykład 0°C, to oznacza, że tylko w 10% obserwacji zanotowano temperatury poniżej lub równe 0°C (a w 90% powyżej tej wartości). Zatem kwantyl 0.1 jest miarą małych wartości jakie może przyjąć analizowany parametr. Analogicznie kwantyl 0.9 charakteryzuje duże wartości danego parametru. Np. jeśli kwantyl 0.9 dla temperatury wynosi 25°C, to oznacza to, że w 90% obserwacji zanotowano temperatury niższe lub równe, a tylko w 10% temperatury wyższe od 25°C. Z kolei kwantyl 0.99 jest często używany jako miara wielkości ekstremalnych (maksymalnych) danego parametru, bo tylko w 1% obserwacji wielkość interesującego nas parametru była większa od tego kwantyla. Podobnie kwantyl 0.01 charakteryzuje ekstremalnie małe (minimalne) wartości parametru.
e. Dystrybuanty prognozy i klimatu modelu
Analiza dystrybuant wyników prognoz wiązkowych wykorzystywana jest w ECMWF do automatycznej detekcji wystąpienie ekstremalnych wielkości istotnych parametrów meteorologicznych w tych prognozach (Lalaurette 2003, Zsoter 2006). Dystrybuanty te tworzy się zbierając wyniki wszystkich elementów wiązki prognoz (np. dla temperatury) dla poszczególnych miejsc i dla określonych czasów wyprzedzenia prognozy, np. dla Warszawy na okres wyprzedzenia równy 5 dni.
Aby wykryć, czy prognoza wiązkowa przewiduje wystąpienie ekstremalnych wielkości jakiegoś parametru meteorologicznego, porównuje się zbiór wyników tej prognozy (dla danego miejsca i czasu prognozy) z czymś, co nazywamy „klimatem modelu”, czyli zbiorem wyników wielu dotychczasowych prognoz tego samego modelu dla tego samego miejsca i tej samej pory roku. Znając ten zbiór, można obliczyć częstość występowania poszczególnych wartości analizowanego parametru meteorologicznego, a następnie jego dystrybuantę charakteryzującą klimat modelu. Możliwe jest teraz porównanie dystrybuanty prognozy modelu z dystrybuantą klimatu tego samego modelu.
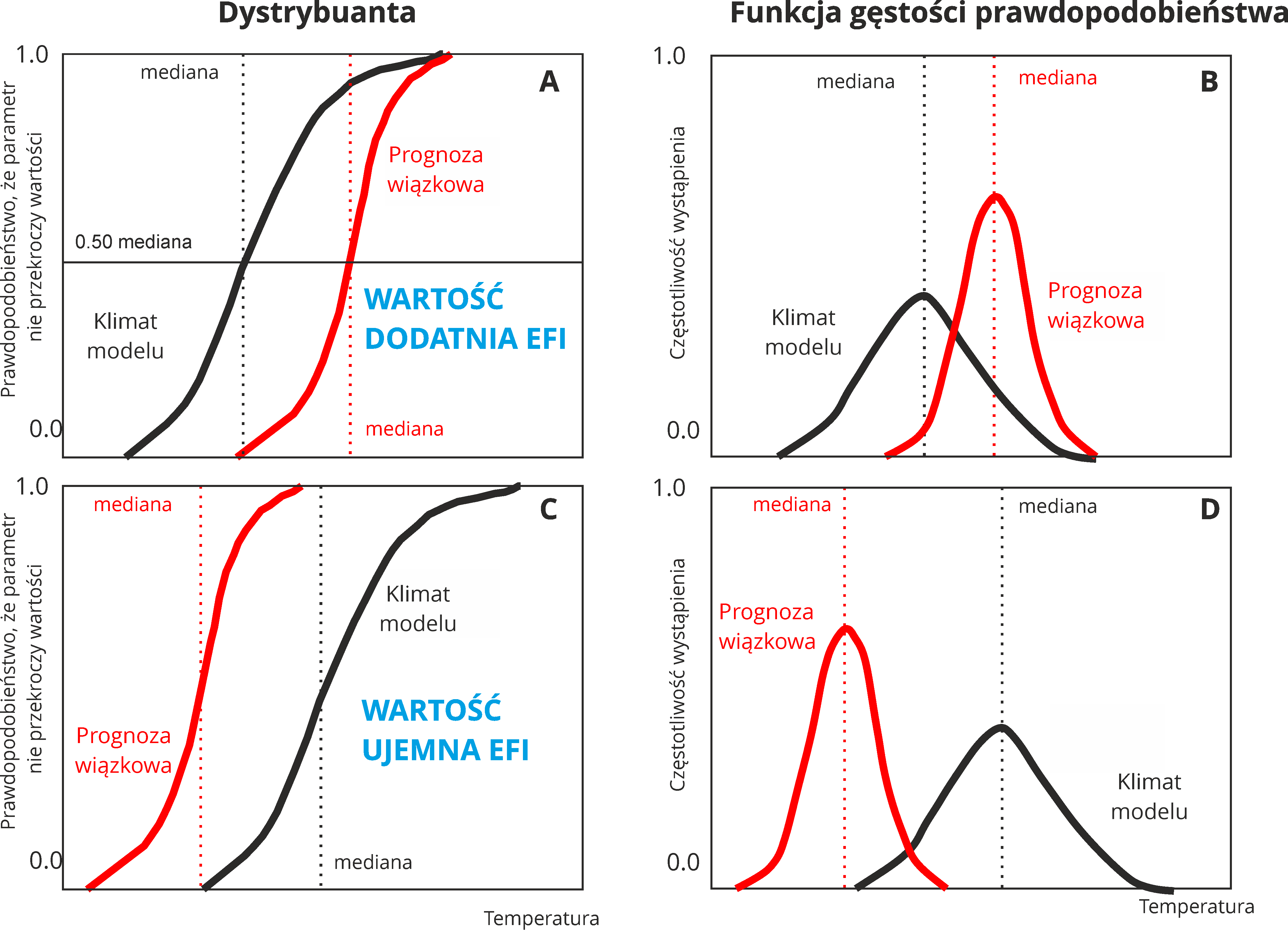
Rys. 12. Dystrybuanta prognozy wiązkowej wraz z dystrybuantą klimatu (A i C), a także funkcja gęstości prawdopodobieństwa (B i D) dla przypadku, gdy prognoza wiązkowa wskazuje wyższe wartości temperatury niż klimat modelu (A i B) oraz dla przypadku, gdy prognoza wiązkowa wskazuje niższe wartości temperatury niż klimat modelu (C i D) (na podstawie confluence.ecmwf.int).
Istotną zaletą tej metody jest to, że porównuje się klimat i bieżące wyniki tego samego modelu, a zatem na wynik porównania nie wpływają błędy modelu, ponieważ tak samo wpływają one na jego prognozę i na jego klimat. Metoda ta jest także uniwersalna w tym sensie, że można ją stosować tak samo do analizy różnych parametrów meteorologicznych, a także dla różnych obszarów o zróżnicowanych cechach klimatycznych, w tym różniących się ekstremalnych wartościach parametrów meteorologicznych (np. w pewnych obszarach temperatury maksymalne mogą osiągać wartości powyżej 35°C, a w innych nie będą przekraczały 20°C).
Wyobraźmy sobie zatem, że wybieramy częstość p dystrybuanty klimatu modelu. Możemy znaleźć jej kwantyl QC(p). Wartość p jest prawdopodobieństwem klimatu modelu, że interesujący nas parametr nie przekroczy wartości QC(p). Znając wartość naszego parametru (np. temperatury), równą QC(p), możemy sprawdzić jaka częstość odpowiada tej wartości parametru na dystrybuancie prognozy wiązkowej. Częstość tę oznaczymy F(p). F(p) jest zatem prawdopodobieństwem prognozy wiązkowej, że interesujący nas parametr nie przekroczy wartości QC(p). Zauważmy teraz, że jeśli dystrybuanta prognozy leży na prawo od dystrybuanty klimatu modelu (czyli kwantyle QF(p) prognozy modelu są większe od kwantyli QC(p) klimatu modelu dla tego samego p), to oznacza, że F(p) jest mniejsze od p. Wynika z tego, że prognoza modelu przewiduje, że jest mniejsze prawdopodobieństwo, że nasz parametr będzie mniejszy lub równy QC(p) w porównaniu z prawdopodobieństwem wynikającym z klimatu modelu. Zatem prognoza modelu daje większe prawdopodobieństwo wystąpienia wielkości większych niż QC(p) w porównaniu z klimatem modelu i ten wzrost prawdopodobieństwa jest równy (p – F(p)). W takiej sytuacji prognoza modelu daje większą szansę na wystąpienie dużych wartości naszego parametru niż daje to klimat modelu. Podobne rozumowanie można powtórzyć dla sytuacji, kiedy dystrybuanta prognozy modelu leży po lewej stronie dystrybuanty klimatu modelu. Wtedy prognoza modelu daje większe prawdopodobieństwo wystąpienia małych wartości naszego parametru, w porównaniu z prawdopodobieństwem wynikającym z klimatu modelu. W takiej sytuacji F(p) jest większe od p i ten wzrost prawdopodobieństwa wynosi (F(p) – p).
f. Definicje wskaźników EFI i SOT
Konstrukcja Extreme Forecast Index (EFI) wykorzystuje wyniki powyższej analizy i za pomocą jednej wielkości całościowo określa, jak różnią się dystrybuanty prognozy i klimatu modelu na całej swojej długości. Wskaźnik EFI zdefiniowany jest następująco (Lalaurette 2003, Zsoter 2006):
EFI
Całkuje on (czyli de facto sumuje) dla wszystkich częstości p od 0 do 1 wyrażenie (p – F(p)), które jest miarą różnicy pomiędzy dystrybuantami klimatu i klimatu modelu i jego interpretacja została omówiona powyżej. Wyrażenie to jest dzielone przez czynnik (p(1 – p))1/2, który spełnia rolę dodatkowej wagi, która znacznie zwiększa wpływ różnic pomiędzy dystrybuantami na wartość EFI w obszarze minimalnych i maksymalnych wartości interesującego nas parametru, czyli dla p bliskich 0 i 1. Dodatkowy czynnik (2/π) jest czynnikiem skalującym, który zapewnia, że absolutna wartość EFI nie przekroczy 1.
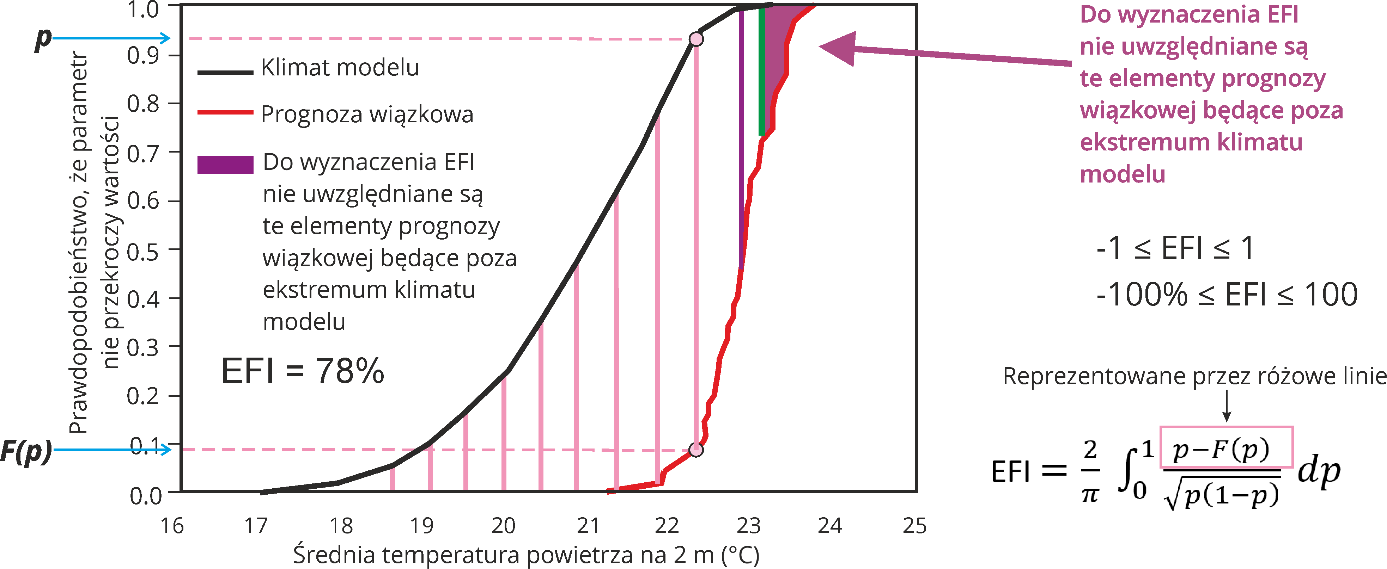
Rys. 13. Dystrybuanta klimatu modelu (czarna krzywa) oraz prognozy wiązkowej (czerwona krzywa) dla temperatury na 2 metrach (na podstawie Tsonevsky i in. (2018)).
Zgodnie z wyżej przedstawioną analizą, jeśli dystrybuanta wyników modelu położona jest na prawo od dystrybuanty klimatu modelu, to wartość (p – F(p)) oraz EFI jest dodatnia, co oznacza że jest większe prawdopodobieństwo wystąpienia większych wartości interesującego nas parametru, niż wynikałoby to z klimatu modelu. I odwrotnie, jeśli dystrybuanta wyników modelu położona jest na lewo od dystrybuanty klimatu modelu, to wartość EFI jest ujemna, co oznacza że jest większe prawdopodobieństwo wystąpienia mniejszych wartości interesującego nas parametru, niż wynikałoby to z klimatu modelu. Generalnie, na podstawie swojej definicji, EFI będzie sumować wpływ różnic pomiędzy dystrybuantami dla wszystkich częstości p, które dla jednych wartości p mogą być ujemne, a dla innych dodatnie. Jednak ze względu na duże wagi, które EFI przykłada do różnicy pomiędzy dystrybuantami w obszarze wartości ekstremalnych analizowanego parametru (czyli tam, gdzie częstości p są zbliżone do 0 lub 1), duże absolutne wartości EFI (bliskie 1) oznaczają duże prawdopodobieństwo wystąpienia wartości danego parametru zbliżonych do ekstremalnych. Wartości EFI zbliżone do 1 oznaczają znaczne prawdopodobieństwo wystąpienia maksymalnych ekstremalnych wartości parametru, a zbliżone do -1 oznaczają znaczne prawdopodobieństwo wystąpienia minimalnych ekstremalnych wartości danego parametru. Jednak duże wielkości EFI dają informację o dużym prawdopodobieństwie przekroczenia ekstremów modelu, ale nie dają informacji jak wielkie mogą to być przekroczenia.
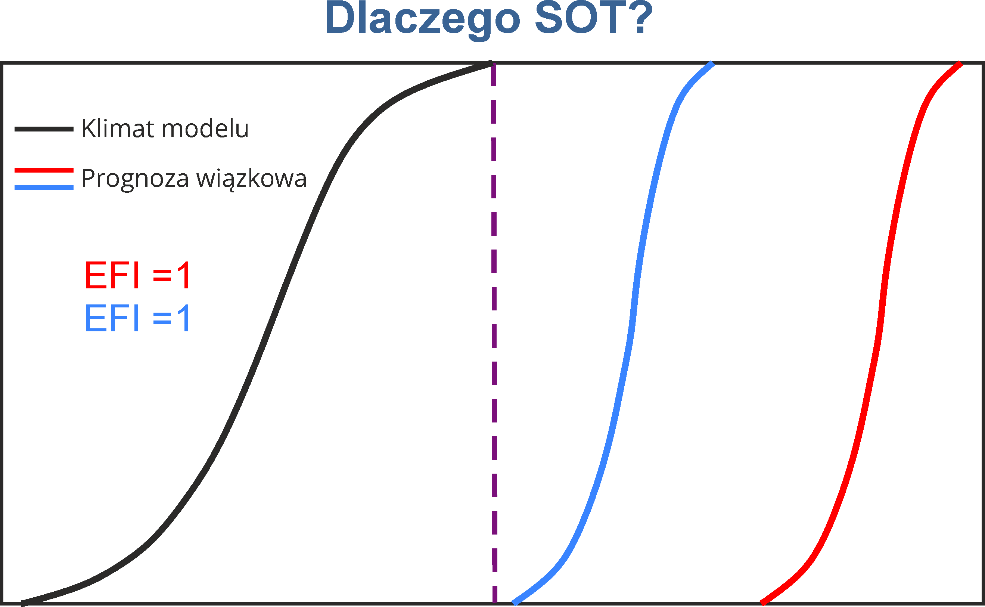
Rys.14. W przypadku gdy prognozowane wartości są wyższe niż ekstrema klimatu modelu, nie mamy informacji jak wielkie mogą to być przekroczenia (na podstawie Tsonevsky (2018)).
Tego typu probabilistycznej informacji udziela dodatkowy wskaźnik o nazwie Shift of Tails (SOT), którego nazwa odnosi się do porównania „ogonów” dystrybuant prognozy i klimatu modelu, czyli do tych ich obszarów, które odpowiadają wysokim i niskim częstościom p (w pobliżu p = 0: „ogon dolny” i w pobliżu p = 1: „ogon górny”). Kwantyle takich częstości odpowiadają ekstremalnym wartościom analizowanych parametrów meteorologicznych (w obszarze „ogona dolnego” wielkościom ekstremalnie małym, a w obszarze „ogona górnego” wielkościom ekstremalnie dużym). Można generalnie powiedzieć, że wskaźnik SOT porównuje na ile „ogon” dystrybuanty prognozy modelu wystaje poza „ogon” klimatu modelu, a zatem jak bardzo ekstremalne wartości prognozy mogą przekroczyć, w sensie probabilistycznym, wartości ekstremalne (maksymalne lub minimalne) charakteryzujące klimat modelu.
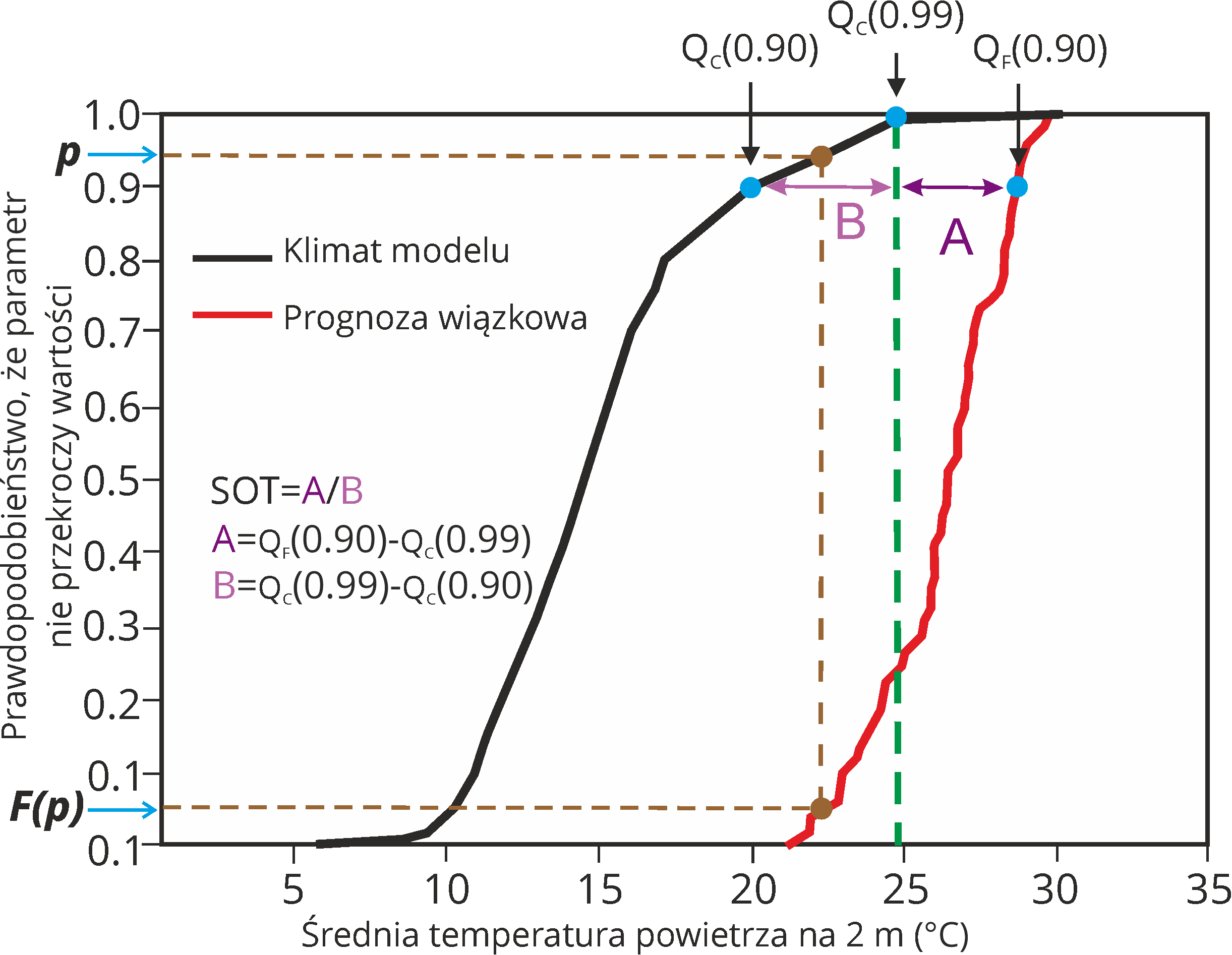
Rys.15. Sposób wyznaczenia wartości SOT (na podstawie Tsonevsky (2018)).
I tak, dla częstości bliskich 1, odpowiadających ekstremalnie dużym wartościom interesującego parametru meteorologicznego, wskaźnik SOT zdefiniowany jest następująco (Zsoter 2006, Tsonevsky 2015):
SOT = (QF(0.90) – QC(0.99)) / (QC(0.99) – QC(0.90))
gdzie QF(0.90) jest kwantylem 0.90 dla prognozy modelu, QC(0.99) jest kwantylem 0.99 dla klimatu modelu, a QC(0.90) jest kwantylem 0.90 dla klimatu modelu. Duże prognozowane wartości parametru meteorologicznego charakteryzowane są tu przez jego kwantyl 0.90, czyli taką jego wartość, że prawdopodobieństwo wystąpienia wartości większej od niej jest uważane za istotne i wynosi 10% (można uważać, że nasza analiza poważnie traktuje możliwość wystąpienia dużej wartości danego parametru, jeśli prognoza wiązkowa daje prawdopodobieństwo wystąpienia tej wartości oraz wartości wyższych w granicach przynajmniej około 10%). Ten kwantyl 0.90 prognozy, czyli QF(0.90), porównywany jest z kwantylem 0.99 klimatu modelu, czyli QC(0.99). Jest to wielkość charakteryzująca wartości ekstremalne klimatu modelu dla danego parametru. Licznik SOT informuje nas zatem jak bardzo kwantyl 0.90 prognozy modelu przewyższa QC(0.99) charakteryzujący maksimum klimatu modelu. Jeśli jego znak (i znak SOT) jest dodatni, to przynajmniej 10% realizacji w prognozie wiązkowej przewiduje, że maksymalne wartości interesującego nas parametru meteorologicznego przekroczą wartość charakteryzującą maksimum dotychczasowego klimatu modelu. Co więcej, im wyższa jego wartość, tym większe jest przekroczenie ekstremum klimatu modelu przez prognozę oraz tym większe jest prawdopodobieństwo takiego przekroczenia. Wyrażenie w mianowniku SOT oblicza jaka jest „szerokość górnego ogona” klimatu modelu, zdefiniowanego jako różnica pomiędzy jego ekstremum, reprezentowanym przez kwantyl 0.99, a kwantylem 0.90. Różnica ta jest wielkością, która skaluje wartość SOT. Zatem SOT wskazuje jak duże jest przekroczenie przez QF(0.90) ekstremum klimatu modelu w stosunku do „szerokości górnego ogona” klimatu modelu. Już wartości SOT powyżej 0 wskazują na istotną możliwość przekroczenia przez prognozę wartości ekstremalnych klimatu modelu, a wielkości istotnie większe wskazują, że takie przekroczenia oraz prawdopodobieństwo ich wystąpienia są wysokie.
Dla częstości bliskich 0, odpowiadających ekstremalnie małym wartościom interesującego parametru meteorologicznego, wskaźnik SOT zdefiniowany jest następująco (Zsoter 2006, Tsonevsky 2015):
SOT = – (QF(0.10) – QC(0.01)) / (QC(0.01) – QC(0.10))
gdzie QF(0.10) jest kwantylem 0.10 dla prognozy modelu, QC(0.01) jest kwantylem 0.01 dla klimatu modelu, a QC(0.10) jest kwantylem 0.10 dla klimatu modelu. Definicja jest analogiczna do poprzedniej, z tym, że teraz małe wartości prognozy charakteryzowane są przez jej kwantyl 0.10, a ekstremalne wartości klimatu modelu przez jego kwantyl 0.01. Teraz ujemne wartości SOT wskazują, że przynajmniej 10% realizacji w prognozie wiązkowej przewiduje, że minimalne wartości interesującego nas parametru meteorologicznego przekroczą (będą mniejsze od) wartości charakteryzującej minimalne ekstremum klimatu modelu. Im mniejsze te wartości, tym większe jest to przekroczenie klimatu modelu oraz większe prawdopodobieństwo jego wystąpienia. Wyrażenie w mianowniku charakteryzuje „szerokość dolnego ogona” klimatu modelu, czyli różnicę pomiędzy jego kwantylem 0.01 charakteryzującym jego ekstremum, a kwantylem 0.10, i jest czynnikiem skalującym SOT. Zatem SOT pokazuje na ile duże jest przekroczenie w prognozie ekstremum klimatu modelu w stosunku do „szerokości dolnego ogona” klimatu modelu. Wartości SOT poniżej 0 wskazują na istotną możliwość przekroczenia przez prognozę ekstremalnie małych wartości z klimatu modelu, a wielkości istotnie niższe wskazują, że takie przekroczenia i ich prawdopodobieństwo są wysokie.
Podstawą powyższych analiz jest wiarygodna informacja o klimacie modelu. Obliczany jest on (Tsonevsky 2015) z wykorzystaniem wiązki 11 prognoz, które obliczają przeszłą prognozę 2 razy w tygodniu, w poniedziałek i czwartek. Prognozy te obliczane są dla tych samych dni w roku wybranych z okresu ostatnich 20 lat. Klimat modelu tworzy się z wyników tych prognoz, które mają miejsce w okresie 5 tygodni obejmującym bieżący tydzień w roku (czyli ten, w którym obliczana jest prognoza operacyjna i dla którego oblicza się EFI i SOT) oraz 2 tygodnie wcześniej i później.
Literatura:
Boisserie, M., L. Descamps, P. Arbogast, 2016, Calibrated forecast of extreme windstorms using the Extreme Forecast Index (EFI) and Shift of Tails (SOT), Weather and Forecasting, 31, 1573—1589
Cox, D., D. Lavers, 2020, Using the EFI for water vapour flux at the UK Met Office Flood Forecasting Centre, ECMWF Newsletter, 165, 9—10
Lalaurette, F., 2003, Early detection of abnormal weather using a probabilistic Extreme Forecast Index, Q.J.R. Meteorol.Soc., 129, 3037–3057.
Magnusson, L., I. Tsonevsky, T. Hewson, 2017, Two storm forecasts with very different skill, ECMWF Newsletter, 154, 4—5
Magnusson, L., F. Wetterhall, F. Pappenberer, 2016, Forecasts showed Paris flood risk well in advance, ECMWF Newsletter, 148, 4—5
Petroligias, T. I., P. Pirson, 2012, Early indication of extreme winds utilising the Extreme Forecast Index, ECMWF Newsletter, 132, 13—19
Richardson, D., I. Tsonevsky, 2012, Application of the new EFI products to a case of early snowfall in Central Europe, ECMWF Newsletter, 133, 4
Tsonevsky, I., 2015, New EFI parameters for forecasting severe convection, ECMWF Newsletter, 144, 27—32
Zsoter, E., 2006, Recent developments in extreme weather forecasting, ECMWF Newsletter, 107, 8—17
Tsonevsky, I., 2018, Extreme Forecast Index, (EFI), Use and interpretation of ECMWF products, Jan-Feb 2018, https://resources.eumetrain.org/data/4/487/mw2018_wednesday_tsonevsky.pdf
Tsonevsky, I., Doswell, C. A., III, & Brooks, H. E., 2018, Early Warnings of Severe Convection Using the ECMWF Extreme Forecast Index, Weather and Forecasting, 33(3), 857-871. doi: https://doi.org/10.1175/WAF-D-18-0030.1
Słownik – najważniejsze pojęcia
Klimat modelu – zbiór wyników wielu dotychczasowych prognoz (historycznych z okresu 20 lat) tego samego modelu dla tego samego obszaru. Klimat modelu tworzy się z wyników prognoz, które mają miejsce w okresie 5 tygodni obejmującym bieżący tydzień w roku (czyli ten, w którym obliczana jest prognoza operacyjna i dla którego oblicza się EFI i SOT) oraz 2 tygodnie wcześniej i później
CAPE (Convectively Available Potential Energy) – Indeks chwiejności atmosfery – opisuje wielkość energii dostępnej dla procesów konwekcyjnych
CAPES (CAPE-SHEAR Parameter) – Indeks chwiejności atmosfery i ścinania wiatru – wskaźnik konwekcyjny – łączący CAPE z informacją o zmienności wiatru z wysokością i odnoszący się do możliwości powstawania szczególnie niebezpiecznych systemów zorganizowanej konwekcji
Atmosferyczny strumień pary wodnej – odzwierciedla obecność tzw. „rzek atmosferycznych” transportujących duże ilości pary wodnej i umożliwiających długotrwałe i obfite opady na stosunkowo dużych obszarach
Udostępnij
